Геометрия на Ялмезе.

В течение многих тысячелетий люди думали, что Земля плоская. Однако наблюдения за тенью Земли во время лунных затмений привели древнегреческих ученых к мысли о шарообразности Земли. Эратосфену удалось даже с довольно большой точностью измерить ее радиус. Но после того, как снова воцарилась мысль, что Земля плоская, для доказательства шарообразности Земли понадобилось кругосветное путешествие Магеллана.

А теперь представьте себе планету Ялмез, где живут разумные существа, но небо закрыто вечной пеленой облаков, а океанские путешествия по тем или иным причинам невозможны. Смогли бы жители этой планеты узнать, что кости, со всех сторон окруженном водой, а на сфере? Иными словами, было ли необходимо путешествие Магеллана для того, чтобы доказать шарообразность Земли?[27]

Чтобы понять, как возникает идея кривизны поверхности, проследим за ходом развития геометрии на планете Ялмез. Геометрия возникает как экспериментальная наука, как теоретическое обобщение многовековых наблюдений над свойствами пространства. Поскольку мы условились считать, что небо планеты покрыто облаками, геометрам Ялмеза пришлось вести наблюдения лишь на поверхности планеты. Оказалось, что среди всех линий, соединяющих две точки этой поверхности, всегда есть наикратчайшая (рис. 1). Наикратчайшие линии и были названы "отрезками прямых". Разумеется, наблюдатель, который посмотрел бы на планету со стороны, сказал бы, что эти линии совсем не прямые, а кривые — это дуги сечений сферы диаметральными плоскостями. Но ялмезяне не могли посмотреть на свою планету со стороны и считали наикратчайшие линии, проведенные на поверхности, прямыми (впрочем, ведь и мы часто говорим "дорога прямая, как стрела", хотя на самом деле она идет по дуге диаметрального сечения).

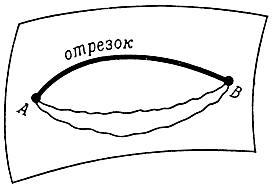
Рис. 1

Затем установили свойства этих "прямых". В самом начале наблюдению была доступна лишь малая часть планеты, а точность измерения оставалась очень небольшой. Поэтому в пределах точности измерения свойства "прямых" на поверхности планеты были такими же, как свойства прямых на плоскости: через две точки проходила одна и только одна "прямая", две "прямые" пересекались в одной и только одной точке (вторая точка пересечения, диаметрально противоположная первой, была недосягаема для наблюдателей). Наконец, ялмезянские геометры были уверены, что их "прямые линии" бесконечны. Самая мысль, что при движении по "прямой" в одном и том же направлении они вернутся в исходную точку, казалась дикой, непонятной и противоречащей здравому смыслу. И ялмезянские ученые были убеждены, что поверхность их планеты бесконечна, а тех, кто выдвигал иные идеи, обвиняли во всех смертных грехах...

Дальнейшее изучение свойств "прямых" показало, что в пределах точности измерения сумма углов любого треугольника равна 180°, что квадрат гипотенузы равен сумме квадратов катетов и т. д. Иными словами, жители Ялмеза построили геометрию Евклида и считали, что она полностью приложима к поверхности их планеты.

Вскоре, однако, им пришлось убедиться, что это не так. По мере развития техники удавалось измерить все большие и большие куски суши (мы договорились, что океанских плаваний ялмезяне совершать не могли). И эти измерения вступили в противоречие с евклидовой геометрией. Чтобы понять, в чем здесь дело, возьмем на сфере три точки A, B и C (рис. 2, а). Эти точки можно соединить "отрезками прямых", а по нашему — дугами меридианов AB и AC и дугой экватора BC. В результате получается треугольник ABC. Легко видеть, что все три угла этого треугольника прямые. Значит, сумма его углов равна 270°, а не 180°, как полагается по геометрии Евклида. На 90° больше, чем нужно.

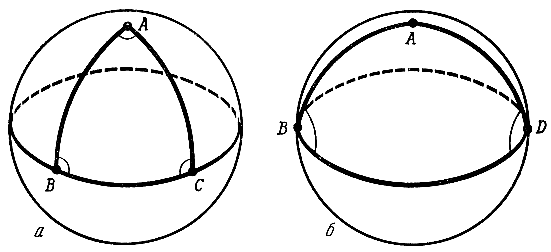
Рис. 2

У других треугольников избыток суммы углов был бы другой. Например, у треугольника ABD (рис. 2, б) углы B и D равны 90°, а угол BAD равен 180°. Сумма углов этого треугольника равна 360° — на 180° больше, чем нужно. В дальнейшем число ?+?+? — 180°, где ?, ?, ? — углы сферического треугольника, мы будем для краткости называть избытком сферического треугольника.