Математический ковер.

Рассказывают, что Екатерина II однажды спросила какого-то генерала, в чем разница между мортирой и гаубицей. Растерявшийся генерал ответил: "А видишь ли, государыня-матушка, мортира-то она особь статья, а гаубица — особь статья". Примерно столь же содержательный ответ можно получить, если спросить далекого от математики человека, в чем разница между линией, поверхностью и телом. Более того, он удивится, как можно спрашивать о столь очевидных вещах. Ведь всякому ясно, что линия, поверхность и тело — совсем разные вещи, и никто не назовет окружность поверхностью или сферу линией.

Но один остроумный шахматный гроссмейстер сказал, что разница между мастером и начинающим шахматистом состоит в том, что начинающему все ясно в позиции, где для мастера все полно тайны. Так же обстоит дело и с нашим вопросом. Конечно, относительно таких геометрических фигур, как квадрат или окружность, ни у кого не возникает сомнений, линии они или поверхности. Но в ходе развития науки после открытий Кантора появилось много самых причудливых геометрических фигур, относительно которых не только школьник, но и умудренный знаниями профессор математики не сразу ответит, что это такое — линия, поверхность или тело.

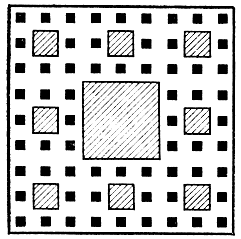
Рис. 19

Вот некоторые из этих фигур. Возьмем квадрат со стороной 1, разделим его на 9 равных квадратиков и выкинем среднюю часть (оставив ее стороны). После этого разделим каждый из оставшихся квадратов снова на 9 равных квадратиков и снова удалим центральные квадратики. Еще один такой шаг приведет к фигуре, изображенной на рис. 19, где заштрихованы все выброшенные квадратики. Ясно, что эта фигура еще является поверхностью. Но мы не остановимся и будем бесконечно много раз делить квадратики на 9 равных частей, после чего выбрасывать среднюю часть. В конце концов у нас получится геометрическая фигура, которую называют ковром Серпинского по имени придумавшего ее польского ученого.

Эта фигура похожа на ткань, сотканную сумасшедшим ткачом. Вдоль и поперек идут нити основы и утка, сплетаясь в очень симметричные и красивые узоры. Но сама получившаяся ткань весьма дырява — ни одного целого куска в ней нет, каждый самый маленький квадратик подвергался вырезанию центральной части. И совсем неясно, чем является этот ковер — линией или поверхностью? Ведь, с одной стороны, он не содержит ни одной целой части, а потому вряд ли является поверхностью, а с другой — образующие его нити сплелись в настолько сложный узор, что вряд ли кто-нибудь без колебаний назовет ковер Серпинского линией. Во всяком случае, нарисовать эту "линию" было бы невозможно.

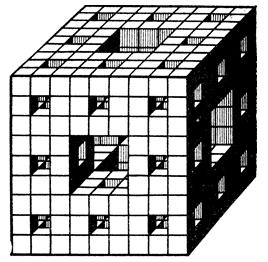
Рис. 20

А ковер Серпинского — не самая сложная из геометрических фигур. Вместо квадрата мы разделим кубик на 27 равных кубиков и выбросим центральный кубик вместе о шестью прилегающими к нему кубиками. После этого разделим каждый оставшийся кубик еще на 27 частей и продолжим операцию выбрасывания (на рис. 20 изображено тело, остающееся после двух выбрасываний). Проделаем эту операцию бесконечно много раз. Чем является оставшаяся после всех выбрасываний геометрическая фигура — линией, поверхностью или телом?