Поворот параллельных.

Но не только наличие избытка у треугольников показало жителям Ялмеза, что они живут не на плоскости, а на кривой поверхности. Неверной оказалась и теорема Пифагора. Например, у треугольника ABC угол А равен 90°, а все его стороны равны друг другу. Вообще, здесь трудно разобрать, где гипотенуза, а где катеты — все углы прямые.

К неожиданным результатам привело и изучение параллельных прямых на поверхности планеты. Ведь если провести на плоскости замкнутую линию, а потом перемещать вдоль нее отрезок так, чтобы он оставался все время параллелен самому себе, то отрезок вернется в исходную точку, не изменив направления (рис. 3, а). Измерения на малых участках поверхности планеты, казалось бы, подтверждали этот результат (параллельными ялмезяне считали прямые, перпендикулярные одной и той же прямой).

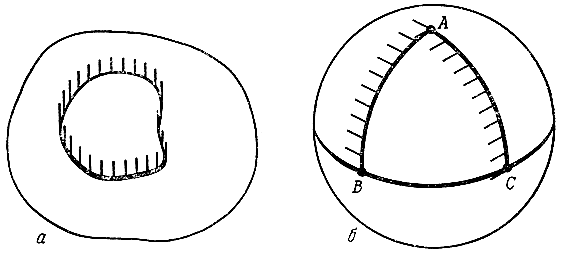
Рис. 3

Ио измерения больших участков поверхности привели совсем к иным результатам. Возьмем, например, треугольник ABC (рис. 3, б) и проведем в точке A "отрезок", перпендикулярный AB. Будем переносить этот отрезок вдоль контура треугольника ABC, следя за тем, чтобы он оставался все время параллельным самому себе. Когда мы придем в точку B, то получим отрезок, направленный по экватору. Так как экватор сам является "прямой", то после параллельного переноса в точку C отрезок снова будет направлен по экватору. А когда мы перенесем его еще по меридиану CA, то получим отрезок, повернутый на 90° относительно первоначального направления (то есть как раз на величину избытка треугольника ABC). А если бы мы переносили отрезок по контуру треугольника ABD на рис. 2, б, то он повернулся бы на 180°.

Вообще, при параллельном переносе по контуру любого сферического треугольника отрезок поворачивается на угол, равный избытку этого треугольника. Любопытный результат получается, если переносить отрезок вдоль экватора. На первый взгляд кажется, что он возвратится в исходную точку, не повернувшись. Но это неверно. Если все время сносить движущийся отрезок в одну и ту же точку — полюс сферы, то мы увидим, что он повернулся на 360° (рис. 4). Но это и неудивительно. Дополним экватор дугой меридиана АВ, пробегаемой в обоих направлениях. Мы получим "треугольник" ABA. В этом треугольнике два угла прямые, а третий равен 360°. Поэтому и его избыток равен 360°.

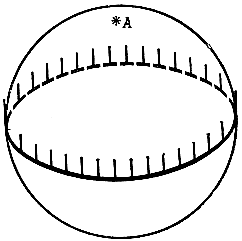
Рис. 4