Области без площади.

Все же разобранный пример еще не слишком убедителен: полученная линия сплошь состоит из точек самопересечения и не ограничивает никакой области. Поэтому возникает вопрос: а может ли "хорошая" кривая, не имеющая точек самопересечения, то есть замкнутая жорданова кривая без самопересечений, иметь ненулевую площадь? Оказывается, может!

Чтобы построить такую кривую, изменим немного проводившееся построение. Сначала построим множество, в котором не только что целого куска плоскости, а и целого куска линии не найдешь, но площадь которого не равна нулю. Для этого надо выбрасывать не только центральные квадратики, а целые кресты, как это показано на рис. 29. При этом размеры удаляемых фигур подберем так, чтобы общая площадь их оказалась меньше половины площади всего квадрата. Тогда на долю остатка придется по крайней мере половина всей площади квадрата. Но при построении остатка мы выбрасывали целые кресты, безжалостно кромсая квадрат. Никакие две точки этого остатка нельзя соединить линией, даже линией в смысле Кантора; всякая связь между его точками отсутствует. Как говорят математики, остаток является вполне несвязным множеством. А площадь этого множества, не содержащего ни целого куска плоскости, ни дуги кривой, отлична от нуля; никакой многоугольной областью, площадь которой меньше ¹/₂, это множество не накроешь.

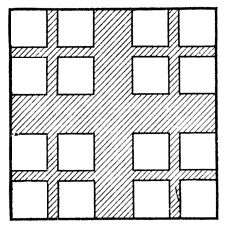
Рис. 29

Теперь уже легко построить пример несамопересекающейся замкнутой кривой, имеющей ненулевую площадь. Для этого нужно соединить полученные точки точно так же, как мы проводили кривую через все точки квадрата. Из-за того, что на каждом шагу мы выбрасывали целые кресты, получающаяся линия не имеет самопересечений (этим она и отличается от кривой Пеано). Но так как она проходит через все точки множества, площадь которого по крайней мере равна ¹/₂, то и площадь полученной линии по крайней мере равна ¹/₂.

Теперь уже ничего не стоит построить область, не имеющую площади. Для этого надо соединить точки А и В полученной кривой какой угодно линией, например полуокружностью. Тогда полученная линия Г ограничивает какую-то область G. Чему же равна ее площадь? Ответ получится разный в зависимости от того, присоединим мы к этой области ее границу или нет — ведь сама граница имеет площадь, по крайней мере равную ¹/₂. Ясно, что обычной площади наша область не имеет. Такие области, не имеющие обычной площади, в математике называют неквадрируемыми.