Счетные множества.

Все множества, которые имеют столько же элементов, сколько имеет множество натуральных чисел, называют счетными. Иными словами, множество называется счетным, если оно бесконечно, но его элементы можно перенумеровать натуральными номерами. Например, множество четных чисел, множество нечетных чисел, множество простых чисел, да и вообще любая бесконечная часть множества натуральных чисел являются счетными множествами.

Иногда, для того чтобы установить счетиость того или иного множества, надо проявить изобретательность. Возьмем, например, множество всех целых чисел (как положительных, так и отрицательных):

..., -n, ..., -3, -2, -1, 0, 1, 2, 3, ..., n, ...

Если мы попробуем нумеровать его по порядку, начиная с какого-нибудь места, то никогда эту нумерацию не закончим. Поэтому все числа до выбранного места останутся незанумерованными. Чтобы не пропустить при нумерации ни одного числа, надо записать это множество в виде двух строк

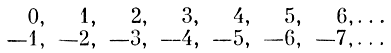
и нумеровать по столбцам. При этом 0 получит № 1, -1 — № 2, 1 — № 3, -2 — № 4 и т. д. Иными словами, все положительные числа и нуль нумеруются нечетными числами, а все отрицательные целые числа — четными. Это похоже на то, как директор гостиницы поместил всех филателистов в гостиницу, заполненную космозоологами.

Но если в то, что множество всех целых чисел счетно, легко поверить, то в счетность множества рациональных чисел поверить труднее. Ведь рациональные числа расположены очень густо — между любыми двумя рациональными числами найдется еще бесконечно много рациональных чисел. Поэтому совершенно непонятно, как их нумеровать; кажется, что между любыми двумя числами надо перенумеровать еще бесконечно много чисел и этот процесс никогда не закончится. И действительно, занумеровать рациональные числа в порядке возрастания их величины невозможно.

Однако если отказаться от расположения рациональных чисел в порядке возрастания, то занумеровать их все же удается. Сделаем так: выпишем сначала все положительные дроби со знаменателем 1, потом все положительные дроби со знаменателем 2, потом со знаменателем 3 и т. д. У нас получится таблица следующего вида:

Ясно, что в этой таблице мы встретим любое положительное рациональное число, и притом не один раз. Например, число 3 встретится и в виде дроби ³/₁, и в виде дроби ⁶/₂, и в виде дроби ⁹/₃.

Теперь приступим к нумерации. Для этого вспомним последний подвиг директора необыкновенной гостиницы, который расселил в ней жителей из бесконечного множества таких же гостиниц. Он тогда воспользовался нумерацией по квадратам. Точно так же поступим и мы, только с тем осложнением, что некоторые дроби будем пропускать (например, так как ¹/₁ получила уже № 1, то дроби ²/₂, ³/₃ и т. д. пропустим: они выражают то же самое число). Получится следующая нумерация положительных рациональных чисел: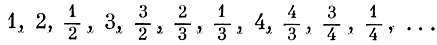

Мы занумеровали, таким образом, все положительные рациональные числа. А теперь уже легко понять, как нумеруются все (то есть положительные и отрицательные) рациональные числа. Для этого надо записать их отдельно в виде двух таблиц и числа одной таблицы нумеровать четными номерами, а второй — нечетными (и еще оставить один номер для нуля).

Вообще, складывая счетное множество счетных множеств, мы снова получим счетное множество. Это доказывается тем же самым приемом нумерации по квадратам.