Как развивалось понятие функции.

Большинство математических понятий прошло долгий путь развития. Первоначально они возникали как обобщение каких-то наглядных представлений, повседневного опыта. Потом из этих наглядных представлений путем отбрасывания частностей и случайных черт выкристаллизовывались точные математические определения. Но часто оказывалось, что эти определения охватывают не только те объекты, изучение которых привело к формулировке данного определения, но и многие объекты, о которых раньше и не думали. Начиналось изучение этих новых объектов, переход к абстракции более высокого уровня, а потом на этой базе — расширение первоначально введенных определений. При этом в математические понятия вкладывался все более широкий смысл, они охватывали все большую совокупность объектов, получали все более разнообразные приложения.

Сложный путь прошло и понятие функции. Идея зависимости некоторых величин восходит, по-видимому, к древнегреческой науке, где она применялась в геометрии. В начале XVII в. Галилей, Кеплер и другие ученые стали развивать кинематику — науку о движении тел.[59] Исходя из этих работ, Декарт ввел в математику общее понятие переменной величины. Фридрих Энгельс так оценивал значение этого события:

"Поворотным пунктом в математике была Декартова переменная величина. Благодаря этому в математику вошли движение и тем самым диалектика и благодаря этому же стало ... необходимым дифференциальное и интегральное исчисление, которое тотчас и возникает и которое было в общем и целом завершено, а не изобретено, Ньютоном и Лейбницем".

С помощью переменных величин ученые XVII в. описывали самые разнообразные движения, в результате чего геометрический язык сменился в математике языком механики. Например, вводя в науку логарифмическую функцию, Непер[60] пользовался изучением движения точек по прямой линии, а Ньютон считал, что математический анализ должен изучать зависимость от времени тех или иных величин, характеризующих движение (пути, скорости, ускорения и т. д.). Впрочем, до поры до времени сохранялся и геометрический язык. Например, рассматривали не тригонометрические функции числового аргумента, а длины некоторых отрезков в круге как функции угла. Даже само понятие функции Лейбниц ввел первоначально как связь между собой некоторых отрезков, характеризующих точки на кривой линии (абсциссы и ординаты, абсциссы и отрезка касательной между точкой касания и осью абсцисс и т. д.).

Но уже в 1718 г. И. Бернулли[61] дал определение функции, свободное от геометрических образов: "Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных". А Эйлер[62] определял функцию так: "Величины, зависящие от других так, что с изменением вторых меняются и первые, принято называть их функциями". Эйлеру же удалось освободить и тригонометрию от геометрического языка — он ввел общее понятие тригонометрической функции числового переменного.

В эпоху Эйлера считали, что функция должна быть выражена единой формулой, в противном случае ее рассматривали как "сшитую" из нескольких функций. Например, функция

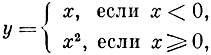
считалась состоящей из двух различных функций.

Вскоре выяснилось, что дело обстоит значительно сложнее. Решая задачу о колебании струны, Д. Бернулли[63] получил ответ в виде суммы бесконечного ряда, членами которого были произведения двух тригонометрических функций, одна из которых зависела от момента времени t, а вторая — от координаты точки струны. Согласно принятому в ту эпоху мнению это означало, что отклонение струны является функцией двух переменных, имеющей, как и положено, единое выражение.

Ту же самую задачу решил Д'Аламбер, но его решение имело совсем иной вид, чем у Бернулли,- при разных значениях аргументов оно задавалось различными формулами. Перед математикой XVIII в. возникло казавшееся неразрешимым противоречие: для одной и той же зависимости получилось два результата, причем один из них для всех значений аргументов выражался одной и той же формулой, а другой — несколькими формулами. Из-за этого решение Д. Бернулли было подвергнуто сомнению: думали, что он нашел не все решения задачи, а лишь решения, выражающиеся одной формулой. Возник ожесточенный спор, в котором приняли участие все крупнейшие математики XVIII в.- Эйлер, Д'Аламбер и др.

По сути дела, спор шел о понятии функции, о связи между функциональной зависимостью и возможностью выразить эту зависимость формулой. Окончательное решение вопроса было получено в начале XIX в., когда Ж. Фурье[64] показал, что сумма бесконечного ряда, состоящего из тригонометрических функций, может на различных участках выражаться различными формулами. После этого он дал новое определение функции, подчеркнув в нем, что главным является задание значений функции, а совершается ли это задание некоторой единой формулой или нет, несущественно.

Результаты Фурье были уточнены немецким математиком Дирихле, который показал, что графиком суммы тригонометрического ряда может быть любая, произвольно проведенная линия. Требуется лишь, чтобы число максимумов и минимумов на этой линии было конечным и линия не поднималась бесконечно высоко.

После длительного обсуждения, в котором приняли участие многие выдающиеся ученые (в том числе Н. И. Лобачевский), стало общепринятым следующее определение функции: "Переменная величина y называется функцией переменной величины x, если каждому значению величины x соответствует единственное определенное значение величины y".

В этом определении ни слова не говорилось о том, что функция должна задаваться одной и той же формулой на всем отрезке, где она определена. С современной точки зрения недочетом этого определения можно считать лишь то, что в нем идет речь о переменных величинах. Ведь с точки зрения "чистой математики" это понятие не имеет четкого определения. В начале XIX в. ученые ограничивались тем, что давали примеры переменных величин, встречающихся в физике (температура остывающего тела, путь или скорость неравномерного движения и т. д.). Они считали, что этим переменным величинам можно поставить в соответствие некую математическую переменную, изменение которой описывает ход изменения физической величины. Но при этом получалось, что одно из основных понятий математики как бы опирается на физическую идею времени.

Создание во второй половине XIX в. теории действительных чисел и построение теории множеств позволили арифметизировать и расплывчатое понятие переменной величины. Оказалось, что под переменной следует понимать букву, вместо которой можно подставлять числа, принадлежащие некоторому числовому множеству X. Разумеется, такой подход к понятию переменной был более статичным, чем принятый у ученых начала XIX в., в нем не было чувства движения, изменения. Но зато он позволил дать определение функции, свободное от лежащих вне математики понятий: "Функцией f, заданной на числовом множестве X, называется соответствие (правило), которое каждому числу x из этого множества сопоставляет число f(x)"

Столь общее определение позволило связать понятие функции с понятиями отображения, преобразования, оператора и т. д. Например, с этой точки зрения, сопоставляя каждому треугольнику его площадь, мы получаем функцию, заданную на множестве треугольников и принимающую значения в множестве положительных чисел. А сопоставляя треугольнику вписанную в него окружность, мы получаем функцию, заданную на том же множестве треугольников, но принимающую значения в множестве окружностей. Поскольку на координатной плоскости и треугольники, и окружности задаются некоторыми наборами чисел, то эти функции можно свести к некоторым числовым функциям. Вообще, числовые функции — один из важнейших видов функций, и потому в дальнейшем изложении мы ограничимся рассмотрением лишь таких функций, да к тому же заданных лишь на числовых множествах.