"Мокрые точки".

У функции, которую мы построили в предыдущем пункте, есть лишь одна точка, около которой бесконечно много максимумов и минимумов, а именно точка 1. Сейчас мы построим другую функцию, у которой таких точек будет куда больше.

Предположим, что на отрезок [0, 1] оси абсцисс падает сверху дождь. Для защиты от дождя поступим следующим образом. Разделим отрезок [0, 1] на три равные части и возведем над средней частью палатку в форме равностороннего треугольника. Она защитит от дождя все точки средней части (кроме концов этой части, то есть точек ¹/³ и ²/₃). Теперь каждую из оставшихся двух частей снова разделим на три равные части и защитим средние части палатками той же формы (но втрое меньшего размера).

У нас получится линия, изображенная на рис. 13. На третьем шаге процесса мы построим еще четыре палатки, потом еще восемь и т. д.

Рис. 13

Возникает вопрос: все ли точки отрезка защищены получившейся пилообразной линией или остались точки, которые дождь намочит? Некоторые из таких "мокрых" точек указать легко — ими являются концы защищаемых отрезков (то есть такие, как ¹/₃, ²/₃, ¹/₉, ²/₉, ⁷/₉, ⁸/₉ и т. д.). Все эти точки остаются без защиты при возведении соответствующей палатки, а последующие палатки их тоже не защищают. Легко видеть, что таких концов будет бесконечное, но счетное множество.

Оказывается, что кроме этого счетного множества "мокрых" точек найдется еще целый континуум таких точек. Чтобы описать их, удобно прибегнуть к троичной системе счисления, в которой все числа записываются с помощью всего лишь трех цифр: 0, 1 и 2. В этой системе счисления число "семь" записывается в виде 21, а дробь ¹/₄ — в виде 0,02020202... (чтобы убедиться в этом, надо вспомнить правило суммирования геометрической прогрессии).

Теперь мы уже можем точно сказать, какие точки останутся "мокрыми" после того, как все защитные палатки будут построены. Первая палатка защищает точки, лежащие между ¹/₃ и ²/₃. Но это те самые точки, которые в троичной системе имеют запись вида

0,1... ,

где точками обозначена любая комбинация цифр 0, 1 и 2 (точно так же, как в десятичной системе счисления между точками ¹/₁₀ и ²/₁₀ лежат все точки, десятичная запись которых начинается с цифры 1, то есть имеет вид 0,1...). После первого шага "мокрыми" останутся точки, троичная запись которых имеет вид

0,0...

или вид

0,2...

Точно так же доказывается, что после возведения двух палаток на втором шаге мокрыми остаются лишь точки, троичная запись которых начинается с одной из следующих четырех комбинаций:

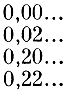
Итак, шаг за шагом защищаются от дождя точки, в троичную запись которых входят единицы. В конце концов останутся "мокрыми" лишь точки, которые можно записать в троичной системе счисления, не используя 1.

А теперь уже ясно, почему множество "мокрых" точек имеет мощность континуума. Ведь это множество можно поставить во взаимно однозначное соответствие с множеством бесконечных телеграмм. Для этого нужно лишь каждой точке вида

0,20220200...

поставить в соответствие бесконечную телеграмму, заменив 0 на точку, а 2 — на тире. При этом разным числам будут соответствовать разные телеграммы. Мы знаем, что множество бесконечных телеграмм имеет мощность континуума. Поэтому и множество "мокрых" точек имеет ту же мощность.

Множество точек, которые мы назвали "мокрыми", впервые построил Кантор, и его называют канторовым множеством. Из построения палаток видно, что около каждой точки канторова множества есть бесконечно много максимумов и минимумов пилообразной линии.