6. РАЗМЕРНОСТЬ КОНЦЕНТРАТА МЕРЫ
Исследование относительной перемежаемости может привести нас и к другим определениям размерности. Вместо множества в метрическом пространстве рассмотрим некую меру ?(S), которая определена в ограниченном подпространстве ? (в соответствующем ? - поле, включающем в себя и шары) и обладает нижеперечисленными свойствами. (А) Когда S - шар, ?(S)>0, а ?(?)=1, т.е. «множество, в котором ?>0» совпадает с пространством ?. (Б) Руководствуясь интуитивными соображениями, можно однако предположить, что мера ? «концентрируется» внутри очень малой части пространства ?. Необходимы новые способы количественного выражения (Б).
При заданных ?>0 и 0<?<1 рассмотрим множества ??, для которых верно неравенство ?(????)<?. Обозначим через N(?,??) инфимум количества шаров радиуса ?, необходимых для покрытия множества ??. Определим
N(?,?)=infN(?,??).
За некоторыми, на мой взгляд, многообещающими эвристическими оценками скрываются выражения «размерностного» вида
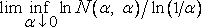 ;
;
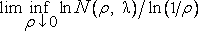 ;
;
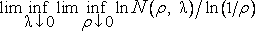 ,
,
строгое исследование которых можно было бы только приветствовать. Разумеется, эвристические оценки заменяют значение infN(?,?) действительным N(?,??) относительно некоторого приемлемого покрытия ??.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК