3. ПОНТРЯГИН И ШНИРЕЛЬМАН. КОЛМОГОРОВ И ТИХОМИРОВ

Среди всевозможных наборов шаров радиуса ?, покрывающих множество S в метрическом пространстве ?, наиболее экономичным по определению является тот, который содержит наименьшее количество шаров. Если множество S ограничено, это наименьшее количество конечно и может быть обозначено как N(?). Учитывая это обстоятельство, Понтрягин и Шнирельман [481] выдвинули в качестве альтернативного определения размерности следующее выражение:

.

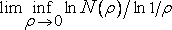Дальнейшее развитие этот подход получил в работе Колмогорова и Тихомирова [278], авторы которой, почерпнув вдохновение в шенноновской теории информации, окрестили величину lnN(?) ? - энтропией множества S. Хокс [204] называет соответствующую размерность нижней энтропийной размерностью, а ее вариант, получаемый заменой liminf на limsup - верхней энтропийной размерностью. Кроме того, Хокс показывает, что размерность Хаусдорфа – Безиковича не может превышать нижней энтропийной размерности; они часто совпадают, но не всегда.

В [278] рассматривается также величина M(?), определяемая как наибольшее количество точек в S, отстоящих друг от друга на расстояние, превышающее 2? . Для множеств, расположенных на прямой, M(?)=N(?). Для других множеств величину

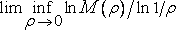
можно считать еще одной размерностью.

У Колмогорова и Тихомирова [278] величина lnM(?) называется емкостью, что в высшей степени неудачно ввиду того, что в теории потенциала уже существует такой термин с совершенно иным и, на мой взгляд, более оправданным значением. В особенности следует избегать искушения определить выведенную в предыдущем абзаце размерность, как емкостную размерность. См. раздел потенциалы и емкости, 3.