УПОРЯДОЧЕННЫЕ СКОПЛЕНИЯ ГАЛАКТИК

Из формулы Pr(U>u)=u^?D мы видим, что субординантная пыль реализует процесс, упомянутый в начале этой главы.

Размерности. Сама пыль имеет размерность D. Если отображения концевых точек каждой линейной паузы соединить интервалами, то получится след Леви; его размерность равна max(1,D) (такую же размерность мы получили, исследуя деревья в главе 16).

Корреляции. След Леви способен линейно упорядочивать порождаемые им галактики; при этом каждая галактика взаимодействует только со своими непосредственными соседями. Каждая же пара соседей ведет себя независимо от других пар. В этом смысле полет Леви сродни ничем не оправданной замене нерешаемой задачи N тел на вполне удобоваримую совокупность многих задач двух тел. Результат мог бы оказаться донельзя нереалистичным, однако не оказался. В работе [383] (полное описание которой можно также найти в монографии П. Дж. Э. Пиблса [467], с. 243 – 249) я показал, что полет Леви приводит к двух- и трехточечным корреляциям на небесной сфере, тождественным тем, которые были получены Пиблсом и Гротом в 1975 г. методом подбора; см. [467].

Рис. 409. В роли художника – ошибка в программе, опус 2

Авторство этой иллюстрации можно частично приписать ошибочному программированию. Ошибку вовремя распознали и исправили (после сохранения результата, разумеется!); конечным результатом вы можете полюбоваться на рис. 105.

Изменения, явившиеся результатом пустяковой ошибки в критическом месте, далеко превзошли наши наихудшие опасения.

Очевидно, что по замыслу в «правильном рисунке 105 должен был наличествовать весьма строгий порядок. Здесь этот порядок оказался скрыт от глаз, причем никакого другого порядка также не наблюдается.

То, что эта иллюстрация – по крайней мере, на первый взгляд – вполне может сойти за произведение высокого искусства, явно не случайно. Свои соображения на этот счет я вкратце высказал в [399] и намерен изложить их в полном виде в самом ближайшем будущем.

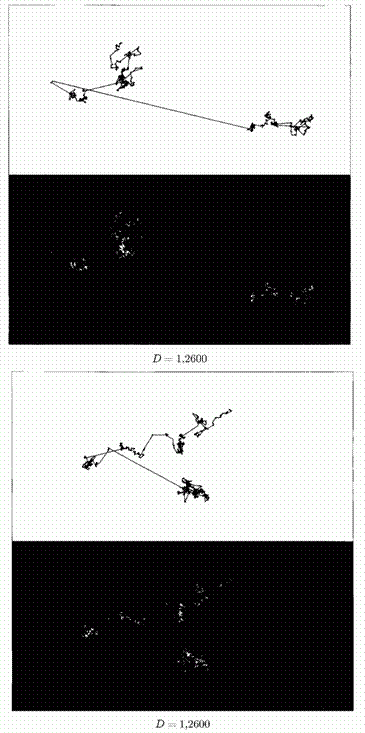
Рис. 410 и 411. Скопления галактик согласно ранней модели Мандельброта (размерность D=1,2600). Полет Леви и его промежуточные остановки

Полет Леви в грубом виде можно представить как последовательность скачков, разделенных остановками. Непосредственный интерес для нас в рамках этой главы представляют последние, однако и скачки являются необходимым элементом построения.

Например, изображенный на верхних (черных на белом) рисунках след движения включает в себя и «инверсионный след», оставляемый летящей ракетой. Трехмерный след показан с помощью двух его проекций на перпендикулярные плоскости. Оригинал можно представить, расположив страницы книги перпендикулярно друг другу.

Нижние рисунки (белые на черном) получены из верхних – в процессе исчезли отрезки, представляющие траектории скачков, а изображение было преобразовано в собственный негатив. Каждая промежуточная остановка символизирует собой звезду, галактику, либо просто некий обобщенный сгусток материи.

Говоря точнее, прямолинейные отрезки на верхних (черные на белом) рисунках имеют следующую особенность: их направление в пространстве случайно и изотропно (т.е. параллельно вектору, соединяющему начало пространственных координат с некоторой точкой, выбранной наугад на поверхности сферы). Различные отрезки статистически независимы, а их длины следуют распределению вероятностей Pr(U>u)=u^?D, за исключением того, что Pr(U>u)=1 при u<1. Значение D=1,2600 близко к значению D~1,23, найденному для реальных галактик.

Подавляющее большинство отрезков слишком малы, чтобы их можно было разглядеть. На самом деле мы просто накрыли плоскость однородной решеткой и отметили те ячейки, на которые приходились одна или более остановок. Иными словами, каждая точка представляет собой целый миникластер.

Кроме того, сами миникластеры также собираются в скопления, причем независимо от значения D. Они демонстрируют настолько ярко выраженные иерархические уровни, что трудно поверить в то, что в рассматриваемую модель не заложено никакой явной иерархии, кроме присущего ей изначального самоподобия.

Для дальнейшего развития темы следует упомянуть и о том, что на всех иллюстрациях в данной подборке представлены начала двух различных полетов, прямого и обратного, и что эти полеты суть не что иное, как две статистически независимые копии одного процесса. Если переместить начало координат в точку какой-либо другой остановки, то и новые половины процесса будут, по всей видимости, независимыми. Следовательно, все промежуточные остановки обладают абсолютно равными правами на звание Центра Мироздания. Эта особенность составляет сущность условного космографического принципа, провозглашаемого мною в настоящем эссе.

Рассматриваемый метод никоим образом не предназначен для объяснения действительного способа образования галактик, однако вполне справляется с продвижением моей основной идеи, заключающейся в том, что условный космографический принцип ничуть не противоречит явной иерархической кластеризации. Можно предложить очень много подобных конфигураций, причем самых разнообразных, пусть даже ни одна из них не окажется «сшита по мерке».

Рис. 412. Неслучайная субординация: кластеризованная фрактальная пыль с размерностью D=1; субординат кривой Коха с размерностью D=1,5

Метод рекурсии, лежащий в основе построения кривой Коха, можно модифицировать так, чтобы кривая систематически терпела разрыв, в результате чего мы получим пыль, обладающую той же размерностью, что и исходная кривая (D=1), но с совершенно иной топологией и внешним видом.

Представьте себе резиновую ленту, первоначально соединяющую концы интервала [0,1], а затем растянутую в виде кохова генератора, с помощью которого мы построили фрактальную кривую с размерностью 3/2 на рис. 81. теперь закрепим резиновую ленту в угловых точках и разрежем посередине каждый из восьми прямолинейных отрезков; получим 16 кусков резины, которые сократятся до своей исходной длины 1/16. Свободные концы этих кусков также закрепим и повторим процесс. Окончательным результатом будет иерархически кластеризованная пыль с r=1/16 и N=16, вследствие чего D=1.

Такой способ построения, по сути дела, позволяет нам заранее пометить все те звенья генератора, которые затем, на следующем этапе кохова построения, будут удалены. В тексте главы этот процесс называется субординацией. В итоге остаются лишь те точки, в которых оказывается движение Коха в моменты времени, принадлежащие некоторому подмножеству с фрактальной размерностью ln16/ln64=4/6. А то, что (4/6)?(3/2)=1, спишем на особый случай правила умножения размерностей, рассматриваемого в соответствующем разделе настоящей главы.

Заметим, что все точки изображенной здесь пыли неизменно упорядочены вдоль кривой Коха, подмножеством которой и является наш генератор. Кроме того, нетрудно найти частотное распределение длин, до которых сокращаются резиновые отрезки, между последовательно расположенными точками закрепления. Количество длин ?u приблизительно пропорционально u^?D, где D=1. Обратите внимание, что на рис. 410 и 411 то же частотное распределение дает совершенно иную картину.

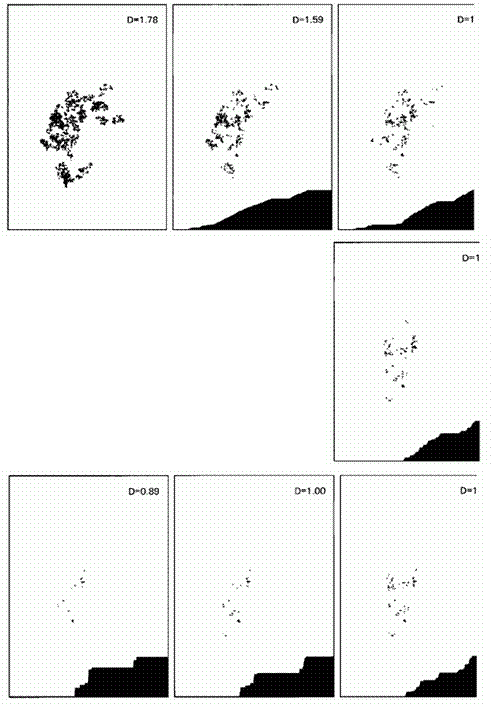
Рис. 414. Понижение размерности D с помощью субординации. Разделение скоплений Леви

Степень кластеризации плоской пыли Леви зависит от ее размерности D. Этот эффект проиллюстрирован здесь путем обработки плоского броуновского следа (D=2) с помощью ряда последовательных субординаций Леви, каждая из которых (кроме первой) применяется к результату предыдущей. В конечном итоге получаем D_{субординатора}=^?1/6=0,89, т.е. последовательность размерностей субординатных пылей имеет следующий вид: 1,78 (=2?0,89), 1,59; 1,41; 1,26; 1,12; 1; 0,89.

Лестницы Леви в правых нижних углах рисунков показывают, какую децимацию пришлось перенести временн?му параметру, чтобы мы могли получить соответствующую пыль из пыли с размерностью D=1,78. При D, близком к 2, еще вполне ясно можно различить «призрак» субординанда (непрерывного броуновского следа), однако при понижении D этот призрак тает прямо на глазах (см. главу 35). Рост кластеризации вызван не сгущением всех точек вокруг немногих центров, а всего лишь исчезновением многих точек, что приводит к росту количества видимых иерархических уровней.

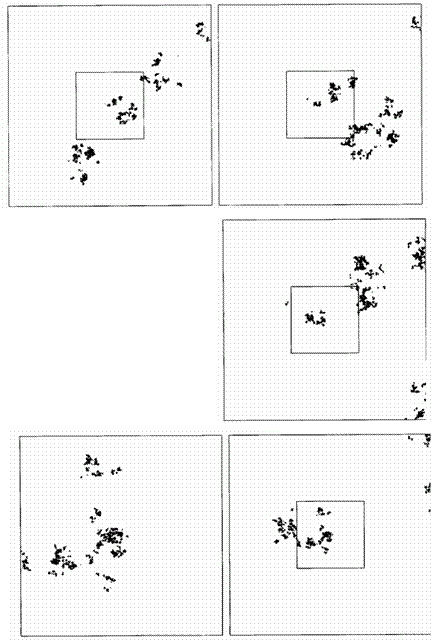
Рис. 415. Пыль Леви с размерностью D=1,2600: крупные планы

Первый рисунок (вверху слева) представляет собой вид из квадратного иллюминатора отдаленного космического корабля на звездное скопление, состоящее из 12 500 000 промежуточных остановок движения Леви. Переход к следующему по часовой стрелке виду символизирует уменьшение расстояния от корабля до центра скопления в b=3 раза, соответственно уменьшается и размер поля зрения. Конструкция, видимая в иллюминатор, меняется в деталях, однако, в общем и целом остается неизменной. Это отнюдь не является для нас неожиданностью – рассматриваемое множество самоподобно.

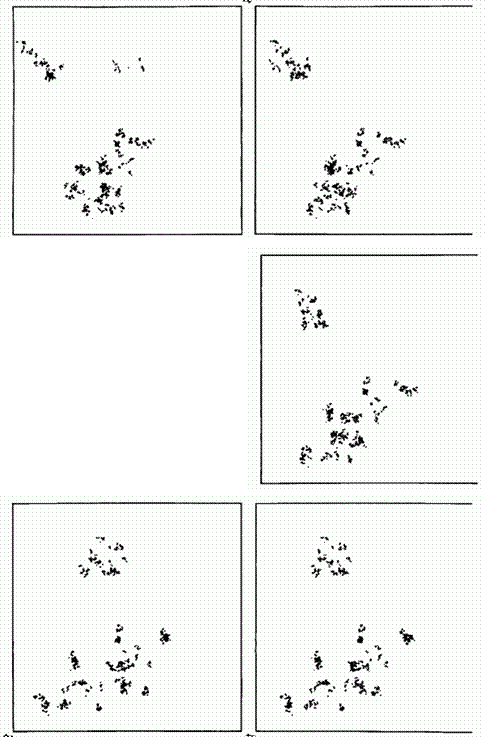
Рис. 416. Круговой облет скоплений Леви с размерностью D=1,3000

Форма скоплений, образованных из остановок полета Леви в плоскости, очень сильно зависит от условий выборки, т.е. при построении большого количества моделей скоплений (пусть и с одинаковой размерностью) следует ожидать не меньшего разнообразия форм.

То же верно и для малого изолированного пространственного скопления Леви при рассмотрении его с различных сторон, что демонстрируют представленные здесь иллюстрации (начиная с верхней левой и далее по часовой стрелке).