СТАНДАРТНАЯ ГЕОМЕТРИЧЕСКАЯ ИНВЕРСИЯ

Следующей по сложности геометрической фигурой после прямой является в евклидовой геометрии окружность, причем окружность остается окружностью не только при преобразовании подобия, но и при преобразовании обратными радиусами, т. е. инверсии. Многие ученые последний раз слышали об инверсии еще в школьные годы, поэтому, на мой взгляд, не лишним будет повторить основные положения. Возьмем окружность C радиуса R с центром в точке O; инверсия по отношению к окружности C преобразует некоторую точку P в точку P', такую, что P и P' лежат на одном луче с началом в точке O, причем длины отрезков |OP| и |OP'| удовлетворяют равенству |OP|?|OP'|=R². Окружности, содержащие точку O, инвертируются в прямые, содержащие точки O, и наоборот (см. рисунок). Окружности, не содержащие точку O, инвертируются в окружности (рисунок внизу справа). Окружности, ортогональные C, и прямые, проходящие через точку O, остаются инвариантными при инверсии относительно C (рисунок внизу слева).

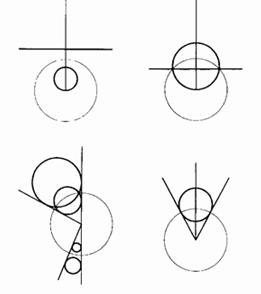
Рассмотрим теперь совокупность трех окружностей: C₁, C₂ и C₃. Обычно – например, когда открытые ограниченные круги, границами которых являются окружности C_m, не пересекаются – существует окружность ?, ортогональная каждой из окружностей C_m. Если окружность ? существует, она совместно самоинверсна относительно C_m.

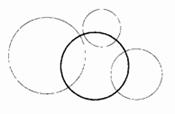
Эти краткие сведения практически исчерпывают то, что стандартная геометрия способна нам поведать о самоинверсных множествах. Остальные самоинверсные множества фрактальны, и большинство из них можно назвать какими угодно, но никак не гладкими.

Генератор. Самоинверсные множества. Как обычно, мы начинаем с генератора, который в данном случае состоит из некоторого (какого угодно) числа M окружностей C_m. Преобразования, представляющие собой последовательность инверсий относительно этих окружностей, составляют то, что алгебраисты назвали бы группой, порождаемой этими инверсиями; обозначим ее буквой G. Для обозначения самоинверсного множества имеется и формальный термин: «множество, инвариантное под действием операций группы G».

Затравки и кланы. Возьмем любое множество S (назовем его затравкой) и добавим к нему преобразования множества S под действием всех операций группы G. Результат, который мы назовем здесь кланом S, является самоинверсным. Хотя, конечно, смотреть тут особо не на что. Например, если множество S представляет собой расширенную плоскость R^? (т. е. плоскость ? плюс точка в бесконечности), то клан S абсолютно идентичен множеству ?^?=S.

Химические инверсные группы. Кроме того, может случиться так, что при некоторой заданной группе G, основанной на инверсиях, клан каждой области S покрывает всю плоскость целиком. В этом случае самоинверсное множество также должно представлять собой всю плоскость целиком. По причинам, которые прояснятся в главе 20, я предлагаю называть такие группы хаотическими. Нехаотическими группами мы обязаны Пуанкаре, однако они носят имя Клейна: дело в том, что Пуанкаре однажды ошибочно приписал какую-то из предыдущих работ Клейна Л. Фуксу; Клейн выразил протест, и Пуанкаре в знак примирения пообещал, что назовет свое следующее великое открытие именем Клейна – и ведь назвал!

Придерживаясь пока нехаотических групп, обсудим три самоинверсных множества, отобранных еще Пуанкаре, затем еще одно множество неясного происхождения и, наконец, пятое, важность которого я обнаружил самостоятельно.