1. КАНТОР И МИНКОВСКИЙ

We use cookies. Read the Privacy and Cookie Policy

Самый приблизительный способ покрытия, восходящий еще к Кантору, заключается в том, что каждая точка множества S объявляется центром шара; объединение этих шаров рассматривается далее как сглаженный вариант множества S и обозначается через S(?).

Добавим сюда допущение о том, что ? является E - мерным евклидовым пространством. В этом случае понятие объема (vol) определено, и можно записать

vol{d?мерный шар радиуса ?}=?(d)?D,

где

?(d)=[?(?)]d/?(1+d/2).

Если S - куб, объем которого много больше ?3, то

vol[S(?)]~vol[S].

Если S - квадрат, площадь которого много больше ?2, то

vol[S(?)]~2??площадь[S].

Если S - интервал, длина которого много больше ?, то

vol[S(?)]~??2?длина[S].

Уточним наше выражение. Введем для обозначения объема, площади или длины общий термин «протяженность», а буквой d обозначим стандартную размерность. Положив

V=vol[S(?)]/?(E?d)?E?d,

мы увидим, что и для кубов, и для квадратов, и для прямых верно следующее выражение:

.

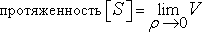Эта формула представляет собой вовсе не пустячное соотношение, связывающее два в равной степени безобидных понятия, как это может показаться на первый взгляд. Как показывает пример, представленный Х. А. Шварцем (1882), по мере увеличения точности триангуляции кругового цилиндра сумма площадей треугольников вовсе не обязательно сходится к площади поверхности цилиндра. Для того, чтобы избежать такого парадоксального поведения, Минковский [431] предпринял попытку свести понятия длины и площади к простой и здравой концепции объема с помощью вышеописанного метода покрытия множества S шарами.

Здесь, однако, с самого начала возникает небольшое затруднение: выражение для V при ??0 может и не иметь предела.

В этом случае предел lim заменяется парой limsup и liminf. Любому вещественному числу A из открытого интервала ]liminf,limsup[ соответствует, по меньшей мере, одна последовательность значений ?m?0, таких, что

.

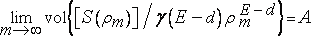Такой последовательности, однако, не существует, если либо A<liminf, либо A>limsup. В соответствии с этими определениями, Минковский [431] называет величины

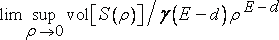
и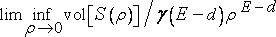

верхней и нижней d - протяженностью множества S. Если они равны, их значение совпадает с d - протяженностью множества S. Минковский также отмечает, что в случае стандартных евклидовых фигур существует некая величина D, такая, что при d>D верхняя протяженность S обращается в нуль, а при d<D нижняя протяженность S бесконечна.