3. ПОТЕНЦИАЛ И ЕМКОСТЬ

Эту связь исследовали Д. Пойа и Д. Серё, в окончательном же виде ее сформулировал О. Фростман в [158]. Главное усовершенствование заключается в том, что рассуждение теперь распространяется не только на точку начала координат ?, но на все точки, принадлежащие множеству S (компактному). Рассмотрим единичную массу, распределенную на множестве S так, что область du содержит массу d?(u). В точке t ядро |u|^?Fдает потенциальную функцию

?(t)=?|u?t|^?Fd?(u).

Для измерения «протяженности» множеств де Ла Вале Пуссен применил физическую концепцию электростатической емкости. Идея такова, что если емкость C(S) множества S достаточно высока, то масса, которую мы можем «перетасовать» для достижения наименее возможного максимального потенциала, равна ?.

Определение. Найдем супремум потенциала по всем точкам t, затем – инфимум полученного результата относительно всех возможных распределений единичной массы на множестве S и, наконец, положим

.

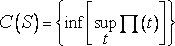Если используется ядро 1/r, то такой минимальный потенциал и в самом деле создается электрическими зарядами на проводящем множестве.

Эквивалентное определение. Величина [C(S)]^?1представляет собой инфимум (среди всех распределений массы, носителем которой является множество S) энергии, определяемой двойным интегралом

??|t?u|^?Fd?(s)d?(t).