λ=1: ДВУСТВОРЧАТАЯ РАКОВИНА.

?=3: дракон Сан-Марко. Своего рода безудержная математическая экстраполяция очертаний венецианской базилики на фоне неба вместе с ее отражением в затопленной пьяцце: я окрестил эту кривую драконом Сан-Марко.

Справа помещена кривая при ?=3,3260680. Это значение ? является ядерным (согласно определению на с. 262) и соответствует периоду w=2. Кривая развернута на 90°, иначе она не входила в отведенные для иллюстрации рамки.

Рис. 266. Обобщение самоквадрируемых фрактальных кривых при вещественных ?

Изображенная на рисунке «драпировка» была построена в памяти компьютера с помощью процесса, который сводится к отсечению от исходного куба всех точек, итерации которых при отображении z??z(1?z) уходят в бесконечность. Параметр ? - вещественное число, изменяющееся в интервале от 1 до 4. Ось ? расположена вертикально, а координаты x и y образуют комплексное число z=x+iy.

Любое горизонтальное сечение представляет собой наибольшую ограниченную самоквадрируемую область с соответствующими значениями параметра ?.

При особом значении ?=2 границей сечения является окружность; будем считать ее «поясом» нашей задрапированной фигуры.

При всех остальных значениях ? границами сечений являются фрактальные кривые, включая и те, что изображены на рис. 264. Можно различить замечательные «складки», расположение которых изменяется в зависимости от ?; ниже пояса они «вдавлены» внутрь, а выше пояса выступают наружу.

Особый интерес представляют наросты на стене, с которой свисает драпировка. К сожалению, данная иллюстрация не может показать сложную структуру верхней части модели во всей ее красе. А). Для каждого значения ? драпировка включает в себя (в качестве своего рода «опоры») фрактальное дерево, составленное из итерированных прообразов точек x - интервала [0,1]. При всех малых и некоторых больших значениях ?<3 ветви этого дерева обладают по всей своей длине некоторой толщиной. Однако при других больших значениях ? от дерева остается лишь голый остов, полностью лишенный толщины. На рисунке мы можем видеть ветви вдоль прямых x=1/2 или y=0, остальные же при данном графическом процессе неизбежно оказываются потеряны. Б). Некоторые горизонтальные участки стены за драпировкой полностью покрыты крохотными «холмами» или «складками», однако мы можем увидеть лишь немногие, самые выдающиеся из них. Эти холмы и складки относятся к «молекулам – островам» (см. рис. 268 и 269), пересекающим вещественную ось. С учетом замечаний А) и Б) теория Мирберга – Фейгенбаума предстает в более общем виде.

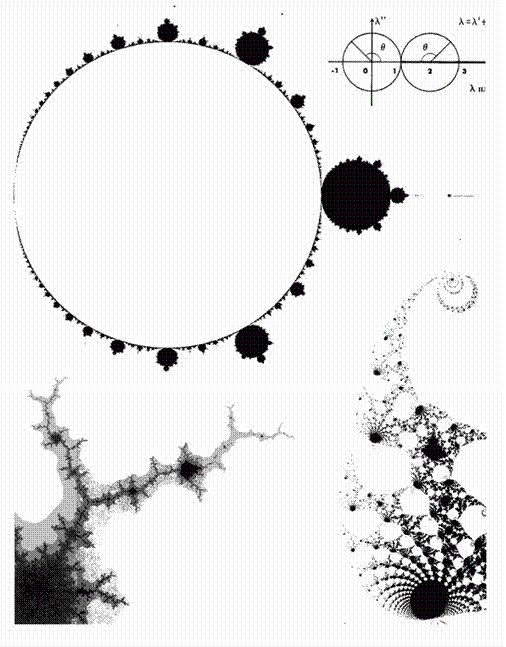
Рис. 268 и 269. Сепараторы отображений z??z(1?z) и z?z²??

Рис. 268 (внизу). ? - отображение. Значения ? внутри замкнутой черной области, ограниченной фрактальной кривой, таковы, что итерации точки z₀=0 при отображении z?z²?? не уходят в бесконечность. Большая точка заострения соответствует точке ?=?1/4, а самая правая точка – точке ?=2.

Рис. 269 (вверху). ? - отображение. Значения ? внутри замкнутой черной области и внутри пустого диска удовлетворяют неравенству Re?>1 и таковы, что итерации точки z₀=1/2 при отображении z??z(1?z) не уходят в бесконечность. Полное ? - отображение симметрично относительно прямой Re?=1.

Диск |??2|?1 и диск |?|?1 без точки ?=0. Значения ? внутри этих областей таковы, что итерации точки z₀=1/2 сходятся к некоторой ограниченной предельной точке.

Корона и отростки. Снаружи пустых дисков ? - отображение образует «корону». Она разбивается на «отростки», «корнями» которых являются «принимающие связи», определяемые как точки вида ?=exp(2?im/n), где m/n - неприводимое рациональное число, меньшее 1.

Рис. 268 (вверху). На рисунке показана часть инверсии ? - отображения относительно точки ?=1. Если внимательно рассмотреть на ? - отображении отростки, корни которых имеют вид ?=exp(2?i/n), может сложиться впечатление, что «соответствующие точки» лежат на окружностях. Рисунок подтверждает истинность этого впечатления. Правильность других кажущихся окружностей подтверждается с помощью других инверсий.

Молекулы – острова. Многие «пятна», возникающие при вышеописанных отображениях, представляют собой истинные «молекулы – острова», о которых впервые сообщается в [398]. Форма такой молекулы идентична форме всего ? - отображения целиком, если не учитывать нелинейного искажения.

Сепаратор, основания и деревья. Граница заполненной черной области при ? и ? - отображениях является связной кривой; так как эту кривую обнаружил я, моим долгом было дать ей имя – я назвал ее сепаратором S. Множество внутри ограниченной этой кривой области разбивается на открытые атомы (см. текст). Обозначив период атома через w, определим его основание как кривую, на которой значение f^*'_w(z_?) вещественно.

Основания, лежащие на вещественной оси, известны в теории самоотображений как интервал [0,1], а их замыкание – как интервал [-2,4].

Словом, я обнаружил, что замыкание других атомных оснований разбивается на совокупность деревьев, каждое из которых укореняется на принимающей связи. В каждой точке такого дерева мы имеем несколько степеней ветвления – степень ветвления для концов ветвей плюс порядки бифуркации, ведущей к корню дерева. Кроме того, когда корень дерева приходится на атом-остров, сюда следует добавить порядки бифуркации, ведущей от дисков |??2|?1 и |?|?1 к этому атому.

Рис. 269 (внизу слева). Здесь представлена подробная картина ? - отображения вблизи точки ?=2?exp(?2?i/3). Множество внутри S представляет собой предел областей вида f_n(1/2)<R, границами которых являются алгебраические кривые, называемые лемнискатами. Показано несколько таких областей, совмещенных друг с другом. При больших n области, равно как и само ? - отображение, выглядят несвязными; в действительности, они связаны, но вне сетки, использованной при вычислениях.

Рис. 269 (внизу справа). Здесь представлена подробная картина ? - отображения вблизи точки ?=2?exp(?2?i/100). У этого стократно ветвящегося дерева и у z - отображения на рис. 270 имеется несколько весьма удивительных общих свойств.

Рис. 271 и 270. Самоквадрируемые драконы; приближение к «пределу Пеано»

Каждая самоквадрируемая кривая привлекательна по-своему. Я, например, нахожу самыми привлекательными «драконов», изображенных на этих рисунках и на рис. С5.

Драконья линька. Дракон, возводящий сам себя в квадрат, представляет собой совершенно бесподобное зрелище! Чудовищная «линька» отделяет бесчисленные складки от кожи на брюхе и спине дракона. Затем она растягивает шкуру на брюхе и спине так, что ее длина – которая, разумеется, и без того бесконечна – увеличивается вдвое! Затем шкура вновь складывается вдоль спины и брюха. И наконец, на последнем этапе, все складки аккуратно водворяются на новые места.

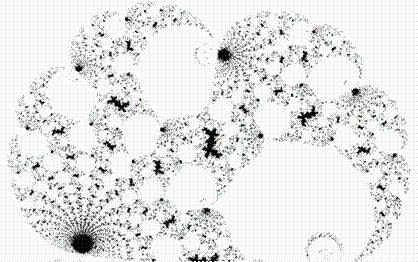
Фрактальная геральдика. Не следует путать самоквадрируемых драконов с самоподобным драконом от Хартера и Хейтуэя (рис. 101 и 102). Читателю предоставляется прекрасная возможность развлечься, отыскивая немногие сходные черты и многочисленные различия.

Последовательные бифуркации. Наилучшие самоквадрируемые драконы получаются, когда точка ? располагается в отростке (см. рис. 269), который соответствует значению ?/2?=m/n, где m и n - малые целые числа. При бифуркации заданного порядка n вокруг каждой точки сочленения появляется драконьих голов – или хвостов, если хотите. Вторая бифуркация порядка m'/n' разбивает каждую из этих областей на n' «сосискообразных» связей и еще более утончает их.

Чтобы получить умеренно упитанного дракона – ни чрезмерно тучного, ни слишком костлявого, - следует поместить точку ? внутри отростка на некотором расстоянии от его корня. Красиво перекрученные драконы получаются, когда точка ? лежит около одного из двух суботростков, соответствующих порядку бифуркации от 4 до 10: один из суботростков дает изгиб влево, другой – вправо.

Рис. 271 (вверху справа). «Истощенный дракон». Дракон, испытавший на себе бесконечное число бифуркаций, теряет всю свою плоть и ссыхается в скелетообразную разветвленную кривую.

Если множество не расходится в бесконечность, его топологическая размерность равна 0 (для пылевидных множеств Фату), 1 (для недоедающих драконов) и 2 (для всех остальных драконов).

Рис. 271 (внизу). ? - дракон. Это множество связно, точка ? лежит на большом «прибрежном острове» с рис. 269 (внизу).

Рис. 270. Особый предел ?=1. Драконы Пеано. Выберем точку ? на острове, расположенном недалеко от связи при ?=2?/n. При n?? величина ??0; следовательно, ? стремится к 1. Форма соответствующего дракона неизбежно должна устремиться к форме двустворчатой раковины (образующей основание задрапированной фигуры на рис. 266). Однако между n=? и n очень большим, но конечным, имеется все же качественное различие.

По мере того, как n??, растет число конечностей дракона, его шкура сминается, а ее размерность при этом возрастает. Вся конструкция представляется этаким «драконом-отшельником», пытающимся забиться внутрь двустворчатой раковины ?=1 и способным заполнить всю ее внутреннюю область без остатка, т.е. размерность дракона стремится к D=2. Что же получается? Самоквадрируемая кривая Пеано? Безусловно; однако, как нам известно из главы 7, кривые Пеано вовсе не являются кривыми. Так происходит и здесь: по достижении размерности D=2 наш дракон прекращает свое существование в виде кривой и перевоплощается в область плоскости.

Рис. 273. Вещественные самоквадрируемые пылевидные множества Фату на интервале [0,1]

Работа Фату [139] представляет собой истинный шедевр в рамках того странного литературного жанра, который называется «заметки в «Отчетах» Парижской Академии наук». Задача пишущего в этом жанре часто сводится к тому, чтобы раскрыть по возможности меньше, но при этом создать впечатление, что автор учел все, что только можно было учесть.

Среди прочих восхитительных откровений, которые лучше всего понимаешь только после тщательного самостоятельного изучения, Фату отмечает следующее: когда число ? вещественно и либо ?>4, либо ?<?2, наибольшее ограниченное множество, остающееся инвариантным при преобразовании x?f(x)=?x(1?x), представляет собой пыль, заключенную в интервале [0,1]. На рисунке показана форма этой пыли при ?>4. По вертикальной оси откладывается величина ?4/? в интервале от ?1 до 5. Концевые точки x₁ и x₂ средней тремы являются решениями уравнения ?x(1?x)=1; на рисунке они образуют параболу. Тремы второго порядка оканчиваются в точках x_1,1, x_1,2, x_2,1 и x_2,2 - таких, что ?x_m,n(1?x_m,n)=x_m, и так далее.

Мне думается, что эта замечательная связь между пылевидными множествами, подобными канторовым, и одной из элементарнейших функций заслуживает самой широкой известности, не ограниченной узким кругом специалистов.