СТАТИСТИЧЕСКИЙ АНАЛИЗ С ПРИМЕНЕНИЕМ НОРМИРОВАННОГО РАЗМАХА R/S
До недавних пор в прикладной статистике принимались как само собой разумеющиеся два следующих допущения в отношении временных рядов: предполагалось, что <X2><? и что случайная величина X обладает краткосрочной зависимостью. Я, однако, показал (см. главу 37), что эмпирические последовательности данных с длинными хвостами часто лучше интерпретируются в свете допущения <X2>=? . С вопросом же о том, является та или иная последовательность данных слабо (краткосрочно) или сильно (долгосрочно) зависимой, мы впервые столкнулись еще тогда, когда я ввел долгосрочную зависимость для интерпретации феномена Херста (см. главу 27).
Такая смесь длинных хвостов и очень долгосрочной зависимости могла бы завести статистиков в тупик, поскольку стандартные методы второго порядка, рассчитанные на неизменную зависимость (корреляцию, спектры), руководствуются допущением <X2><?. Есть. Однако, альтернатива.
Можно пренебречь распределением величины X(t) и проанализировать ее долгосрочную зависимость с помощью нормированного размаха; иначе такая процедура называется R/S - анализом. Этот статистический метод, предложенный в [408] и получивший математическое обоснование в [384], основан на различии между краткосрочной и очень долгосрочной зависимостями. В этом методе вводится постоянная J, которая называется коэффициентом Херста, или R/S - показателем, и может принимать любые значения в интервале от 0 до 1.
Значимость постоянной J можно описать еще до ее определения. Особое значение J=? характерно для независимых, марковских и других случайных функций с краткосрочной зависимостью. Таким образом, для того, чтобы узнать, присутствует ли в эмпирических данных или в выборочных функциях очень долгосрочная непериодическая статистическая зависимость, достаточно проверить, приемлемо ли статистически предположение J=?. Если нет, то такая зависимость присутствует, а мера ее интенсивности определяется разностью J??, значение которой можно оценить на основании имеющихся данных.
Главное достоинство такого подхода заключается в том, что показатель J устойчив по отношению к маргинальному распределению. То есть он эффективен не только в тех случаях, когда последовательности данных или случайные функции являются почти гауссовыми, но и тогда, когда распределение X(t) настолько далеко от гауссова, что <X2(t)> расходится, а в этом случае не работает ни один из методов второго порядка.
Определение статистического R/S - размаха. В непрерывном времени t определим X*(t)=0?tX(u)du, X2*(t)=0?tX2(u)du и X*2=(X*)2. В дискретном времени i определим X*(0)=0 и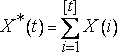 
; здесь [t] - целая часть t. Для всякого d>0 (величину d назовем запаздыванием) определим скорректированный размах суммы X*(t) на временн?м промежутке от 0 до d в виде
.
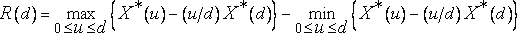Оценим далее выборочное среднеквадратическое отклонение величины X(t):
S2(d)=X2*(d)/d?X*2/d2.
Величина Q(d)=R(d)/S(d) называется статистическим R/S - размахом или самонормированным самокорректированным размахом суммы X*(t).
Определение R/S - показателя J. Предположим, что существует некоторое вещественное число J, такое, что при d?? величина (1/dJ)[R(d)/S(d)] сходится по распределению к некоторой невырожденной предельной случайной величине. Как доказано в [384], из этого предположения следует, что 0?J?1. В этом случае говорят, что функция X имеет R/S - показатель J и постоянный R/S - префактор.
Сделаем более общее предположение: пусть к некоторой невырожденной предельной случайной величине сходится по распределению отношение [1/dJL(d)][R(d)/S(d)], где L(d) - некоторая медленно изменяющаяся на бесконечности функция, т.е. функция, удовлетворяющая условию L(td)/L(d)?1 при d?? для всех t>0. Простейшим примером такой функции является L(d)=lnd. В этом случае говорят, что функция X имеет R/S - показатель J и R/S - префактор L(d).
Основные результаты [384]. Когда X(t) - белый гауссов шум, имеем J=? и постоянный префактор. Если точнее, то отношение e??JR(e?)/S(e?) является стационарной случайной функцией от ?=lnd.
В более общем виде, равенство J=? справедливо во всех случаях, когда S(d)?<X2>, а нормированная сумма a??X*(at) при a?? слабо сходится к B(t).
Когда X(t) - дискретный дробный гауссов шум (т.е. последовательность приращений функции BH(t), см. с. 488), имеем J=H, где H?]0,1[.
В более общем виде, для получения J=H?? и постоянного префактора достаточно, чтобы S(d)?<X2> и чтобы сумма X*(t) приближалась к функции BH(t) так, что <X*(t)>~t2H.
В еще более общем виде, значение J=H?? и префактор L(d) преобладают, если S(d)?<X2>, а X*(t) приближается к функции BH(t) и удовлетворяет соотношению <X*2(t)>~t2HL(t).
И наконец, J??, если S(d)?<X2>, а X*(t) приближается к некоторой негауссовой масштабно-инвариантной случайной функции с показателем H=J. Примеры можно найти в [551, 554, 555].
С другой стороны, если X - белый устойчивый по Леви шум (т.е. <X2>=?), то J=?.
Когда функция X в результате дифференцирования становится стационарной, то J=1.