4. СЛУЧАЙНОЕ ВЗВЕШЕННОЕ СТВОРАЖИВАНИЕ [378, 376]

В работах [378, 376] я предложил естественное и достаточно глубокое обобщение метода Безиковича, которое получило дальнейшее развитие в [254].

Воздействие каждого этапа каскада заключается в умножении плотностей в b³ субвихрях каждого вихря на одинаково распределенные и статистически независимые случайные веса W_i.

После k этапов каскада взвешенного створаживания количество вихрей, в которых оказывается сосредоточена б?льшая часть массы, составляет величину порядка b^kD* (при общем количестве вихрей b^3k), где

D^*=?<Wlog_b(r³W)>=3?<Wlog_bW>.

В частности, если величина W дискретна и ее возможные значения w_i имеют относительные вероятности p_i, имеем

D^*=3??p_iw_ilog_bw_i.

Случай D^*>0; D=D^*. Мера, порождаемая взвешенным створаживанием аппроксимируемого фрактально однородной мерой с размерностью D=D^*, получаемой так же, как описано в главе 23.

Случай D^*<0; D=0. Количество непустых ячеек асимптотически стремится к нулю, а это значит, что предел почти наверное оказывается пустым.

В общей сложности, носитель массы аппроксимируется замкнутым множеством с размерностью D=max(0,D^*).

Сечения. Аналогичным образом масса, заключенная в плоских и линейных сечениях, сосредотачивается в относительно малом количество вихрей: b^D*?1 для плоских сечений (при общем числе вихрей b²) и b^D*?2 для линейных сечений (при общем числе вихрей b). То есть сечения невырождены при D^*>1 (и, соответственно, D^*>2) и аппроксимируются фракталами с размерностями D^*?1 и D^*?2. Таким образом, размерности сечений в этом случае подчиняются тем же правилам, что и в случае лакунарных фракталов.

Новые случайные величины, инвариантные при взвешенном сложении. Пусть X - это случайная величина, которая асимптотически задает вес, заключенный внутри вихря любого порядка k или внутри его сечения прямой или плоскостью (размерность сечения обозначим через ?). Я показал, что величины X удовлетворяют функциональным уравнениям

,

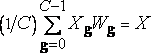где C=b^?, величины W_g и X_g - независимые случайные величины, равенство же выражает идентичность распределения. Это уравнение представляет собой обобщение уравнения (L), рассматриваемого в разделе устойчивые по леви случайные величины и функции. Решения этого уравнения являются обобщением устойчивых случайных величин и подробнее обсуждаются в цитированных выше статьях [378, 376] и [254].