2. ХАУСДОРФОВА МЕРА

Хаусдорф [203] расширяет определение Каратеодори, допуская возможность дробного значения d (функция ?(d) записывается таким образом, что она при этом продолжает иметь смысл). Таким образом, мы больше не ограниченны степенями ?, а вольны использовать любую положительную пробную функцию h(?), которая стремится к нулю вместе с ?.

Более того, поскольку шар представляет собой всего лишь множество точек, расстояние до которых от центра w не превышает заданного радиуса ?, шар продолжает оставаться определенным даже в случае неевклидова пространства ? - при условии, что в этом пространстве определено расстояние. Как мы уже отмечали, такие пространства называются метрическими, следовательно, и хаусдорфова мера представляет собой метрическое понятие.

Если задана некоторая пробная (или «калибровочная») функция h(?), то можно сказать, что мера конечного покрытия множества S шарами радиуса ?_m равна ?h(?_m). Для получения наиболее экономичного покрытия мы рассматриваем все покрытия шарами, радиус которых меньше ?, и образуем инфимум

.

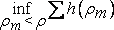При ??0 ограничение ?_m<? становится чрезвычайно жестким. То есть выражение inf?h(?_m) может только возрастать; у него есть предел, который имеет вид

.

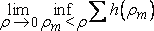Этот предел может быть конечным положительным, отрицательным или нулевым. Он определяет h - меру множества S.

Если h(?)=?(d)?^d, то h - мера называется d - мерной. Точнее говоря, из-за префактора ?(d) h - мера является нормированной d - мерной мерой.

Если h(?)=1/ln|?|, то h - мера называется логарифмической.