9. УСТОЙЧИВЫЕ ПО ЛЕВИ ВЕКТОРЫ И ФУНКЦИИ

Заменим случайную величину X в функциональном уравнении (L), участвующем в определении устойчивости, случайным вектором X. Если задан некоторый единичный вектор V, то очевидно, что система уравнений (L) и (A:D) имеет элементарное решение – произведение вектора V на скалярную устойчивую случайную величину.

Леви [304] показывает, что общее решение есть просто сумма всех элементарных решений, каждое из которых соответствует своему направлению в пространстве и взвешено в соответствии с некоторым распределением по поверхности единичной сферы. Вклады этих решений могут быть дискретными (конечными или счетно бесконечными), либо бесконечно малыми. Для того, чтобы вектор X был изотропным, элементарные вклады должны быть распределены равномерно по всем направлениям.

Устойчивые по Леви векторные функции от времени. Подобно устойчивым скалярным функциям, векторные функции допускают разложение в сумму скачков, следующих гиперболическому распределению. Размеры и направления скачков определяются распределением по поверхности сферы.

Распределение Хольтсмарка. Спектроскопические исследования Хольтсмарка [220] пережили свое время благодаря тому, что их результаты оказалось возможным переформулировать в терминах ньютоновского притяжения (см. [76]); до появления моих работ только в этих исследованиях фигурировал конкретный пример устойчивого по Леви распределения. Предположим, что в точке O имеется некая звезда, а в пространстве распределено (независимо друг от друга и с ожидаемой плотностью ?) еще некоторое количество звезд единичной массы. Какова общая сила притяжения, испытываемая звездой O со стороны этих звезд? Вскоре после того, как Ньютон открыл свой знаменитый обратно - квадратичный закон притяжения, преподобный Бентли написал ему письмо, в котором указал на то, что притяжение звезд, заключенных внутри узкого конуса d?' с вершиной в точке O, имеет бесконечное математическое ожидание; то же можно сказать и о притяжении звезд, заключенных внутри узкого конуса d?'', симметричного конусу d?' относительно точки O. Бентли заключил, что разница между этими бесконечностями не определена.

При решении задачи Хольтсмарка (в том виде, в каком ее обычно формулируют) подобная трудность нам не грозит, так как здесь мы имеем дело не с самими математическими ожиданиями, а с разностями между действительными и ожидаемыми величинами притяжения. Для начала рассмотрим звезды, заключенные внутри области, ограниченной вышеописанным конусом угловой величины d? и сферами радиусов r и r+dr. Каждая звезда притягивает с силой u=r^?2, а их количество представляет собой пуассонову случайную величину с ожиданием ?|d?|d(r³)=?|d?|d(u^?3/2). Следовательно, для разности между действительным притяжением и его математическим ожиданием имеем характеристическую функцию

.

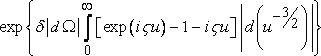Как выясняется, эта разность соответствует устойчивой по Леви случайной величине с показателем D=3/2 и ?=1 . Из подраздела 6 (см. выше) нам известно, что большое положительное значение u обусловлено, скорее всего, присутствием одной – единственной звезды вблизи точки O и не зависит от плотности звезд в других местах; распределение случайной величины U при очень больших u ведет себя как распределение величины притяжения ближайшей звезды.

Таким образом, общее избыточное притяжение представляет собой изотропный устойчивый по Леви вектор с D=3/2.

Смысл устойчивости можно объяснить так: допустим, звезда O испытывает притяжение со стороны двух равномерно распределенных звездных облаков, состоящих, скажем, из красных и голубых звезд; тогда величины силы притяжения только красных звезд, только голубых звезд и всех звезд вместе различаются лишь масштабным коэффициентом, а не аналитической формой их распределения.