ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ ИСКЛЮЧИТЕЛЬНО КАК МЕРА ФРАГМЕНТАЦИИ

Вышеописанное построение допускает следующее изменение генератора:

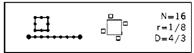
Общая величина D остается неизменной, однако береговая размерность D_c принимает наименьшее возможное значение, D_c=1. То есть в рамках этой модели береговые линии островов могут быть спрямляемы! В этом случае общая величина D определяет не степень иррегулярности, а единственно степень фрагментации. Размерность D характеризует здесь не извилистость отдельных кривых, а целое соотношение между количеством прямоугольных островов в бесконечном семействе и их площадью.

При измерении длины кривой шагом ? результат все еще стремится к бесконечности при ??0, однако теперь для этого имеется другая причина. Шагом длины ? можно измерять только острова, диаметр которых не меньше ?. Однако по мере того, как ??0, число таких островов возрастает, и измеренная длина изменяется пропорционально ?^1?D — точно так же, как и в отсутствие островов.

В общем случае D_c>1, значение D_c характеризует только степень иррегулярности, в то время как D описывает степень иррегулярности и фрагментации в совокупности.

Фрагментированная фрактальная кривая может иметь касательные в любой точке. Закруглив углы островов, можно добиться того, что к береговой линии в любой ее точке можно будет провести касательную, причем площади островов — а с ними и общая размерность D — останутся неизменными. Таким образом, фрактальность ?- кривой и отсутствие у кривой касательных — вовсе не одно и то же.