МАСШТАБНО-ИНВАРИАНТНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

Вернемся, однако, к более серьезным вещам. Для того чтобы получить возможность говорить о масштабно-инвариантных случайных величинах, следует определить термин «масштабно-инвариантный» без привлечения геометрии. Дело в том, что единственной геометрической фигурой, которую можно поставить в соответствие случайной величине, является точка, а точка на части не делится. В качестве приемлемой замены можно предложить следующий вариант: будем говорить, что случайная величина X масштабно - инвариантна при преобразовании T(x), если распределения X и T(x) тождественны во всех отношениях, кроме масштаба.

Термин «преобразование» понимается здесь в широком смысле: например, сумма двух независимых реализаций случайной величины X рассматривается как результат преобразования X. Соответствующие величины следует называть масштабно-инвариантными при сложении, но мы будем называть их устойчивыми по Леви (см. главы 31, 32 и 39). В главе 39 (с. 501 и 528), кроме того, упоминаются и случайные величины, масштабно-инвариантные при взвешенном сложении.

Асимптотический скейлинг. Асимптотически гиперболические С. В. К счастью, приведенное выше определение вовсе не является столь неопределенным, как может показаться на первый взгляд. При многих преобразованиях, как выясняется, для инвариантности требуется асимптотически гиперболическое распределение. Это означает, что должен существовать некоторый показатель D>0, такой, что пределы

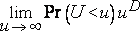и

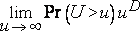
определены и конечны, причем один из них положителен.

Распределение Парето. Термин «асимптотически гиперболическое распределение» можно рассматривать как синоним термина, хорошо знакомого статистикам-экономистам, а именно: распределение Парето. Вильфредо Парето – итальянский экономист, который пытался перевести законы механического равновесия в термины равновесия экономического, однако более прочно его имя запомнят, вероятнее всего, в связи с открытием им фундаментальной статистической закономерности: он обнаружил, что в определенных обществах количество индивидуумов с личным доходом U, превышающим некую большую величину u, распределяется приблизительно гиперболически, т.е. пропорционально u^?D. (Несколько позже в этой главе мы еще вернемся к распределению доходов.)