АПОЛЛОНИЕВЫ СЕТИ САМОИНВЕРСНЫ

Вернемся к началу построения аполлониевой сети: трем касательным окружностям. Добавим сюда любую из соответствующих аполлониевых окружностей и назовем получившиеся четыре окружности ? - окружностями. Все четыре показаны на нижеследующем рисунке жирными линиями.

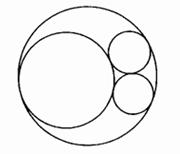
Существует четыре комбинации из трех ? - окружностей (мы будем называть их триплетами), и каждой из них соответствует окружность, ортогональная каждой окружности триплета. Возьмем эти новые окружности в качестве генератора и обозначим через C₁, C₂, C₃ и C₄ (на рисунке ниже они показаны тонкими линиями). А ? - окружность, ортогональную окружностям C_i, C_j и C_k, обозначим как ?_ijk.

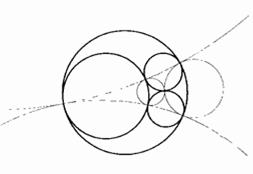
Разделавшись с нудным развешиванием ярлыков, получаем заслуженную награду. Даже самое поверхностное рассмотрение показывает, что наименьшее (замкнутое) множество, самоинверсное по отношению к четырем порождающим окружностям C_m, представляет собой аполлониеву сеть, построенную на четырех ?-окружностях. Любопытно, что об этом наблюдении никто явным образом не сообщает, хотя оно должно быть известно довольно широко.

При более тщательном изучении мы увидим, что каждая окружность в сети преобразуется в одну из ?-окружностей, проходя через уникальную последовательность инверсий относительно окружностей C. Таким образом, принадлежащие аполлониевы сети окружности можно рассортировать на четыре клана, причем клан, нисходящий от окружности ?_ijk, мы будем обозначать как G?_ijk.