5. ПРЕДЕЛЬНОЕ ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОЕ СЛУЧАЙНОЕ СТВОРАЖИВАНИЕ И ФУНКЦИЯ [367]

В [367] описана вихревая решетка, сочетающая в себе абсолютное и взвешенное створаживание, позаимствованное у Кантора. Вихри не задаются заранее, но генерируются при построении с помощью того же статистического механизма, который используется для генерации заключенной в них массы. Кроме того, дискретные вихревые слои сливаются в такой решетке в непрерывный континуум.

Предельная логарифмически нормальная функция: обоснование. Произведем кое-какие последовательные модификации взвешенного створаживания на примере некоторой функции L(t) от одной переменной (выбранной из соображений простоты).

После n - го этапа плотность взвешенного створаживания задается функцией Y_n(t), такой, что приращение ?lnY_n(t)=lnY_n+1(t)?lnY_n(t) есть ступенчатая функция; изменяется эта функция только тогда, когда tпредставляет собой интеграл, кратный b^?n=rⁿ, в остальные же моменты времени ее значениями являются независимые случайные величины вида lnW. Положим теперь, что приращение ?lnW является логарифмически нормальным со средним ??(lnb) и дисперсией ?lnb. При этом ковариация между ?lnY_n(t) и ?lnY_n(t+?) принимает на интервале |?|<rⁿ значение ?(lnb)(1?|?|/rⁿ) и обращается в нуль вне этого интервала. Функция ?lnY_n(t) не может считаться гауссовой, поскольку совместное распределение ее значений при двух (или более) t не является многомерной гауссовой случайной величиной.

Первая модификация. Заменим все ?lnY_n(t) соответствующими ?lnY^*_n(t), определяемыми как гауссовы случайные функции с практически той же ковариацией ?(lnb)exp(1?|?|/rⁿ). В результате такой замены сохраняется «область зависимости» оригинала, однако нарушаются дискретные границы между вихрями продолжительности rⁿ.

Вторая модификация. Заменим дискретный параметр nlnb непрерывным параметром ?. Сумма конечных разностей ?lnY^*_n(t) заменяется при этом интегралом бесконечно малых дифференциалов dlnL_?(t) со средним ???d? и дисперсией ?d?, а вихри становятся непрерывными.

Определение функции L(t). Рассмотрим предел

.

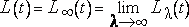Случайная величина lnL_?(t)является гауссовой со средним <lnL_?(t)>=???? и дисперсией ?²L_?(t)=??. Отсюда <L_?(t)>=1 при всех ?. Однако предел функции L_?(t) может быть либо невырожденным, либо почти наверное равным нулю. Математического разрешения эта проблема пока не получила, однако можно, очевидно, придать строгий вид нижеследующим эвристическим рассуждениям. Они проводятся на примере более интересных функций L(x) от трехмерной переменной.

Множество концентрации предельной логарифмически нормальной меры. Удобным средством для получения представления о множестве, в котором значение L_?(x) не только не мал?, но чрезвычайно велико, являются опорные квадраты со стороной rⁿ. Это не искусственно навязанные субвихри, а всего лишь способ измерения. При n?1 и фиксированном x вероятность того, что значение логарифмически нормальной функции L_{n lnb}(x) окажется очень близко к нулю, чрезвычайно высока, т.е. на б?льшей части области определения значения этой функции чрезвычайно малы.

Поскольку функция L_{n lnb}(x) непрерывна, изменение ее значения внутри ячейки со стороной rⁿ очень невелико, а это значит, что к настоящей модели применим способ получения множества концентрации в случае взвешенного створаживания с логарифмически нормальной величиной W. Если пренебречь логарифмическими членами, то количество ячеек, составляющих б?льшую часть интеграла функции L_{n lnb}(x), имеет математическое ожидание Q=(rⁿ)^D*, где D^*=3??/2.

Если ?>6 (т.е. D^*<0), то Q?0 при ???, и функция L(x) почти наверное вырождена.

Если 4<?<6 (т.е. 0<D^*<1), то функция L(x) имеет размерность D=D^* и невырождена, однако ее следы на плоскостях и прямых почти наверное вырождены.

Если 2<?<4 (т.е. 1<D^*<2), то функция L(x) и ее следы на плоскостях невырождены (размерности D^* и D^*?1, соответственно), однако ее следы на прямых почти наверное вырождены.

Если 0<?<2 (т.е. 2<D^*<3), то и функция L(x), и ее следы на плоскостях и прямых невырождены (размерности D^*, D^*?1 и D^*?2, соответственно).