ЛУННЫЕ КРАТЕРЫ И КРУГОВЫЕ ТРЕМЫ

Начнем с одного второстепенного вопроса, который обеспечит нас упрощенной двумерной подготовкой и сам по себе довольно занимателен: какова геометрическая природа множества, не занятого лунными кратерами? Хотя греки называли словом ??????чашу или иной сосуд для питья, большая часть кратеров на поверхности Земли имеет вулканическое происхождение. Большинство людей, однако, полагает, что кратеры, наблюдаемые на поверхности Луны, Марса, юпитерианского спутника Каллисто, а также других планет и их спутников образовались, преимущественно, в результате падений метеоритов.

Чем больше метеорит, тем шире и глубже оказывается образующийся при его ударе о поверхность планеты кратер. Кроме того, большой кратер, явившийся следствием падения тяжелого метеорита, может «стереть с лица планеты» несколько уже существовавших малых кратеров; с другой стороны, падение легкого метеорита вполне может оставить «зазубрину» на краю старого большого кратера. Что касается размеров кратеров, существуют достоверные эмпирические данные в пользу того, что площади кратеров (измеренные сразу же после удара метеорита о поверхность) следует гиперболическому распределению: количество кратеров, площади которых превышают s км2 , а центры расположены в пределах квадрата со стороной в 1 км2 , можно записать в виде C/s, где C - некоторая константа. За подробностями отсылаю к работам [411], [8] и [200] .

Для упрощения рассуждений (главный результат от этого не изменится) аппроксимируем лунную поверхность плоскостью, а лунные кратеры – тремами в форме кругов. Если бы Луна вечно захватывала метеориты из статистически инвариантного окружения, то каждая точка ее поверхности снова и снова оказывалась бы принадлежащей какому – либо кратеру, и так до бесконечности. С другой стороны, те или иные геологические процессы – такие, скажем, как выход на поверхность вулканической лавы – могут время от времени «стирать» кратеры, и в этом случае трема – множество, не покрытое на какой-то момент времени кратерами, может оказаться весьма нетривиальным. Кроме того, эволюция солнечной системы могла происходить таким образом, что бомбардировка Луны метеоритами заняла лишь какой-то конечный период времени. Параметр C может характеризовать либо время, прошедшее после последнего стирания кратеров, либо общую продолжительность бомбардировки.

Для оценки влияния параметра C на форму трема – фрактала попробуем изменить этот параметр, сохраняя инвариантной затравку. По мере увеличения C от 0 до 2 поверхность Луны становится все более насыщенной кратерами, а размерность D свободной от кратеров поверхности, согласно одному из выводов предыдущего раздела, уменьшается и достигает нуля при C?2. Зависимость формы трема – фрактала от D проиллюстрирована на рис. 424 – 427.

Аппенцеллер и Эмменталер. При очень малых значениях параметра C наши фракталы представляются мне (думаю, многие любители швейцарских сыров со мной в этом согласятся) похожими на ломтики сыра, почти целиком испещренные очень маленькими, «булавочными» отверстиями. Можно назвать такую форму приблизительной экстраполяцией структуры аппенцелльского сыра. По мере увеличения C мы постепенно переходим к столь же приблизительной экстраполяции структуры другого сыра, эмментальского, для которого характерны большие, перекрывающие друг дружку отверстия.

(Вот так выясняется, что английский детский стишок о Луне, сделанной из зеленого сыра, является истинным отражением реальности – за исключением, пожалуй, цвета.)

Топология. Критические значения D. Обе упомянутые выше экстраполяции могут быть лишь приблизительными, поскольку площадь трема – фрактальных «ломтей сыра» приближается к нулю. Выскажу предположение: пока параметр C достаточно мал, трема – фрактал представляет собой ? - кластер, каждый из контактных кластеров которого имеет вид переплетения связанных между собой нитей с топологической размерностью D_T=1. Когда размерность D достигает определенного критического значения D_крит, размерность D_T падает до нуля и ? - паутина коллапсирует в пыль.

Следующее критическое значение D=0. При C>2 поверхность Луны перенасыщена кратерами – любая из ее точек почти наверное принадлежит, по меньшей мере, одному кратеру. Так, в частности, обстояло бы дело, если бы поверхность Луны никогда не очищалась от кратеров и продолжала бы бесконечно принимать на себя удары метеоритов.

Немасштабируемые кратеры. Плотность кратеров, покрывающих поверхности некоторых других планет (наша Луна в их число не входит), характеризуется выражением вида Ws^??, где ??1. С задачей, которую ставят перед нами такие кратеры, мы разберемся в приложении к настоящей главе.

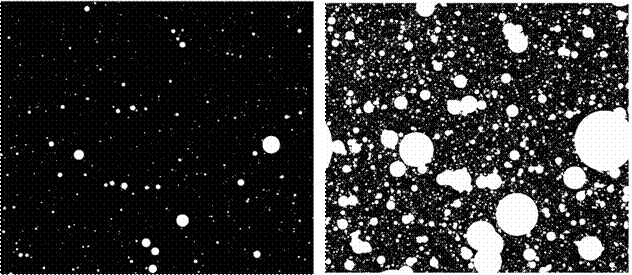
Рис. 424 и 425. Малые круговые тремы (белые) и случайные «швейцарские сыры» (размерности D=1,9900 и D=1,9000)

Тремы на этих иллюстрациях представлены в виде белых кругов. Их центры распределены на плоскости случайным образом. Площадь круга ранга ? равна K(D?2)/?; выбор числовой постоянной осуществляется, исходя из соображений соответствия трема – модели, описанной в тексте главы. На рис. 424 мы видим нечто похожее на сыр аппенцеллер в разрезанном виде (размерность черной области D=1,9900), поверхность же, изображенная на рис. 425, напоминает об эмментальском сыре (размерность черной области D=1,9000).

Рис. 426 и 427. Большие круглые тремы (черные) и случайные разветвленные белые нити (размерности D=1,7500 и D=1,5000)

Построение этих фигур сходно с построением фигур, изображенных на рис. 424 и 425, только здесь тремы черные, а их площадь больше (настолько больше, что свободного места почти нет). Под D подразумевается размерность белой фрактальной области, оставшейся невырезанной.