ДИАМЕТРИЧЕСКИЙ ПОКАЗАТЕЛЬ Δ

Леонардо да Винчи пишет в своих «Заметках» (заметка № 394): «Совокупная толщина всех ветвей дерева на любой высоте равна толщине ствола (ниже их)». Формальное выражение выглядит следующим образом: диаметры ветвей настоящего дерева до и после разветвления (d, d₁ и d₂)

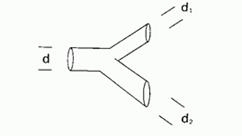
удовлетворяют соотношению

d^?=d₁^?+d₂^?,

где ?=2. Смысл этого выражения таков: если принимать во внимание толщину ветвей, настоящие деревья не являются самоподобными деревьями с почти заполняющей пространство корой. В самом деле, самоподобие требует выполнения равенства ?=D, а размерность D почти заполняющей пространство структуры должна быть близка к E=3.

Иными словами, во всех случаях, когда выполняется вышеприведенное соотношение, величина ? представляет собой новый параметр в дополнение к размерности D; мы будем называть этот новый параметр диаметрическим показателем. Его рассматривали очень многие люди – в большинстве случаев независимо друг от друга – в этом можно убедиться, взглянув хотя бы на список литературы в [568]. В этой главе показано, что для бронхов ?~3. Показатель ? дерева артерий равен приблизительно 2, 7, а для настоящих деревьев он близок к значению, указанному Леонардо, ?=2. Ширина рек также регулируется показателем ?=2. Кроме того, мы рассмотрим здесь некоторые физические, физиологические и геометрические аспекты величины ?.

Параразмерность. Во «Фракталах» 1977 г. я называл показатель ? паразмерностью (от греческого ???? «рядом, около»), но я больше не настаиваю на употреблении этого термина. Функции величины ? вообще весьма туманны: в одних случаях она является размерностью, в других – нет. Аналогичное поведение демонстрирует показатель в [29]; см. также главу 39.