НЕСТАНДАРТНЫЙ СЛУЧАЙ, δ=0

Представим теперь обратную ситуацию – такую, в которой вспомогательное допущение ложно, а точнее, в которой предел 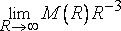обращается в нуль. В этом случае абсолютное распределение вероятностей указывает лишь на то, что некий случайно выбранный шар конечного радиуса R почти наверняка окажется пустым. А значит тот, кто сидит на выбранной в пространстве случайным образом точке и глазеет по сторонам, почти наверняка ничего не увидит. Однако вероятностное распределение масс интересно человеческим существам лишь в той степени, в какой оно объясняет положение дел в реальной Вселенной, где как известно, масса в нуль не обращается, по крайней мере, в окрестности места обитания этих самых существ. После того, как событие произошло, абсолютная вероятность именно этого события представляет весьма ограниченный интерес.

Тот факт, что неусловное распределение автоматически пренебрегает подобными случаями, говорит о вопиющей его неадекватности при ?=0. Оно не только не совместно с массой, содержащейся в любом фрактале с размерностью D<3, но и не сообщает нам абсолютно ничего, кроме того, что ?=0.

Условное распределение вероятностей, напротив, проводит четкие границы между фракталами с разными фрактальными размерностями, между масштабно-инвариантными и масштабно-неинвариантными фракталами, а также между разными прочими допущениями.