7. НЕСТАНДАРТНЫЕ ЦЕНТРАЛЬНЫЕ РЕДЕЛЫ. РОЛЬ ГИПЕРБОЛИЧЕСКИХ СЛУЧАЙНЫХ ВЕЛИЧИН

Дана бесконечная последовательность X_n, составленная из независимых и одинаково распределенных случайных величин. Центральная предельная задача формулируется следующим образом: возможно ли выбрать такие веса a_n и b_n, чтобы сумма 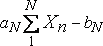имела нетривиальный предел при N???

В стандартном случае <X_n²><? ответ на этот вопрос будет стандартен и утвердителен: a_N=1/?N, b_N~<X_n>?N, а предел является гауссовым.

Нестандартный случай <X_n²>=? намного сложнее: а) выбор a_N и b_N не всегда возможен; б) когда выбор возможен, предел оказывается устойчивым негауссовым; в) для того, чтобы показатель предела был равен D, достаточно, чтобы последовательность X_n имела асимптотически гиперболическое распределение с показателем D (см. главу 38); г) необходимое и достаточное условие приводится в источниках, перечисленных в начале этого раздела.