АНОНС: ЛАКУНАРНОСТЬ

Даже после того, как мы добавим к размерностям D_T и D степень ветвления R, фрактал остается во многих отношениях недостаточно определен. Особое значение имеет еще одно дополнительное свойство, которое я назвал лакунарностью. Пустоты в очень лакунарном фрактале имеют очень большой размер, и наоборот. Основные определения можно было бы привести и здесь, однако мне представляется более целесообразным отложить это до главы 34.

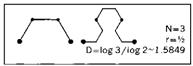
Рис. 205. СТРЕЛА СЕРПИНСКОГО (РАЗМЕРНОСТЬ ГРАНИЦЫ D ~1,5849)

В [522] Серпинский строит кривую, инициатором которой является интервал [0, 1], а генератор и второй терагон выглядят следующим образом:

Последующие этапы построения имеют вид:

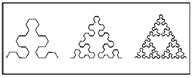
О том, как будет выглядеть эта кривая на одном из поздних этапов построения, можно получить представление, взглянув на очертания «береговой линии» в верхней части рис. 205 (над самым большим черным тр еугольником).

Самокасания. Конечные приближения кривой не имеют точек самокасания (как в главе 6), однако предельная кривая содержит бесконечно много таких точек.

Стрелы, заполняющие плоскость. Стрела на рис. 205 (если положить ее набок, она будет больше похожа на тропическую рыбу) определяется как участок кривой Серпинского между двумя последовательными возвращениями в точку самокасания — в данном случае, в середину интервала [0, 1]. Такими стрелами можно заполнить плоскость; при этом соседние стрелы соединяются друг с другом в этакой безумной экстраполяции застежки Велькро. (Или, возвращаясь к предыдущей метафоре, плавники одной рыбы в точности помещаются между плавниками двух других рыб.) Кроме того, сплавив вместе четыре должным образом выбранных соседних стрелы, мы получим точно такую же стрелу, увеличенную вдвое.

Тремы салфетки Серпинского. Я называю кривую Серпинского салфеткой по альтернативному способу ее построения, который основан на вырезании «трем» — метод, широко используемый в главах 8 и 31- 35. Мы получаем салфетку Серпинского, имея в качестве инициатора, генератора, а также двух последующих этапов построения следующие замкнутые множества:

Этот трема-генератор содержит в себе вышеприведенный линейный генератор в качестве собственного подмножества.

Водораздел. Впервые я столкнулся со стрелой Серпинского — правда, тогда я еще не знал о Серпинском — при изучении формы одного водораздела [381].

Рис. 207. АСИММЕТРИЧНАЯ ФРАКТАЛЬНАЯ ПАУТИНА (РАЗМЕРНОСТЬ D=2)

Эта паутина получается рекурсивным построением из замкнутого тетраэдра (инициатора) и совокупности четырех меньших тетраэдров (служащих генератором).

Ее размерность D=2. Попробуем спроецировать ее вдоль линии, соединяющей середины любой из пар противоположных ребер. Проекцией тетраэдра-инициатора будет квадрат, который мы назовем исходным. Каждый тетраэдр второго поколения проецируется на подквадрат, длина стороны которого составляет 1/4 от длины стороны исходного квадрата, и т. д. Таким образом на исходный квадрат проецируется вся паутина целиком. Границы подквадратов перекрываются.

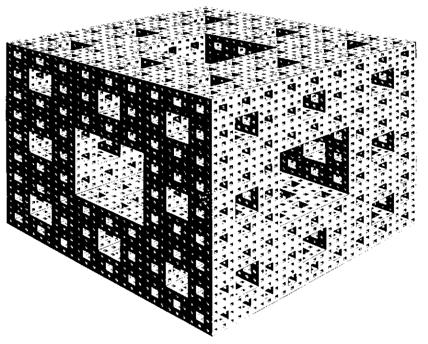
Рис. 208. КОВЕР СЕРПИНСКОГО (РАЗМЕРНОСТЬ D~1,8928) И ГУБКА МЕНГЕРА (РАЗМЕРНОСТЬ D~2,7268)

Ковер Серпинского. В [523] Серпинский строит кривую, инициатором которой является сплошной квадрат, а генератор и два следующих терагона представлены ниже:

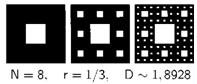
Площадь такого ковра обращается в нуль, а общий периметр его пустот стремится к бесконечности.

Рис. 208. Губка Менгера. Принцип построения очевиден. Продолжая построение до бесконечности, мы получим некий остаток, называемый губкой Менгера. Я сожалею о том, что в своих предыдущих эссе ошибочно приписал ее авторство Серпинскому. (Рисунок воспроизводится по книге Леонарда М. Блюменталя и Карла Менгера «Геометрические этюды» с любезного разрешения ее издателей, компании W. Н. Freeman & Со. © 1970.) Пересечения губки с медианами или диагоналями исходного куба являются троичными канторовыми множествами.

Сливающиеся острова. Как ковер, так и салфетку Серпинского можно получить и другим способом — еще одним обобщением рекурсии Коха, допускающим самоперекрытия, которые, однако, учитываются только единожды.

Для получения салфетки инициатором следует взять правильный треугольник, а генератором — фигуру, изображенную слева на приведенном ниже рисунке. Для получения ковра в качестве инициатора возьмем квадрат, а генератором послужит фигура, изображенная справа.

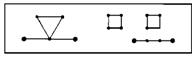
Здесь мы снова встречаемся с двумя феноменами, знакомыми нам по главе 13: береговая линия каждого острова спрямляема, следовательно, размерность ее равна 1, размерность же салфетки или ковра выражает скорее степень фрагментации суши (т. е. степень ее разделенности на острова), нежели степень неправильности береговых линий островов.

В остальном результат совершенно нов: в главе 13 море представляет собой связное множество, что выглядит как должная топологическая интерпретация открытых морских пространств. Оно открыто и в смысле топологии множеств, т. е. его граница ему не принадлежит. Новизна, привнесенная настоящим построением, заключается в том, что коховы острова могут теперь асимптотически «сливаться» в некий сплошной сверхостров, однако континента из него не получается, а береговые линии образуют в сочетании решетку.

< С точки зрения топологии, всякий ковер Серпинского является плоской универсальной кривой, а губка Менгера представляет собой пространственную универсальную кривую. То есть (см. [38], с. 433 и 501) эти фигуры оказываются самыми сложными кривыми соответственно в плоскости и в пространстве любой более высокой размерности. ?

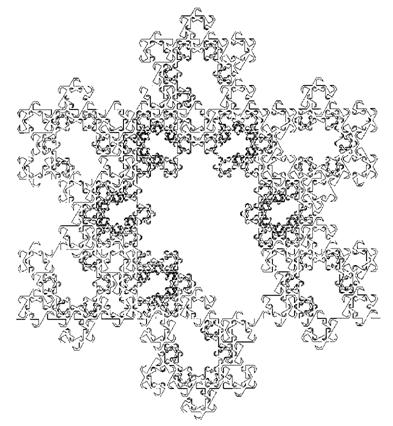
Рис. 210. РАСКОЛ В СНЕЖНЫХ ПАЛАТАХ (РАЗМЕРНОСТЬ D ~1,8687)

Давным-давно в далекой стране в прекрасных Снежных Палатах восседал Великий Правитель со своею свитой. Однако между его подданными произошел раскол, за ним последовала война, в которой ни одна из сторон не одержала верх. И тогда Мудрые Старейшины провели границу, разделившую Палаты надвое, дабы туда могли войти без опасения ступить на враждебную территорию и представители Севера, и представители Юга.

Загадки лабиринта. Кто контролирует Великую Палату и как можно войти в нее снаружи? Почему некоторые малые палаты оказываются несориентированы ни по какой стороне света? Подсказку можно найти на обезьяньем дереве на рис. 55.