СТВОРОЖЕННАЯ СЛУЧАЙНАЯ ЛИНЕЙНАЯ ПЫЛЬ

Более удобное определение створаживания (предложенное в [378], где я называю его каноническим) можно получить с помощью последовательности случайных двоичных выборов, каждый из которых определяется простым броском монеты. Бросок монеты на первом этапе решает последующую судьбу каждого из bподынтервалов. Если выпадает орел (событие с вероятностью p<1), то данный подынтервал «выживает» как часть предтворога; в противном случае мы с ним больше не встретимся. Изолированные точки, остающиеся между «мертвыми» подынтервалами любой длины, после каждого этапа стираются. Здесь, конечно, от них вреда немного, однако их плоскостные или пространственные аналоги (изолированные линии и т.д.) порождают в множестве ложную связность. Ожидаемое количество выживших подынтервалов равно <N>=pb=p/r. Далее процесс возобновляется, причем каждый подынтервал обрабатывается независимо от других.

Формализм процесса рождения. Если назвать подынтервалы «детьми», а весь каскад – «семьей», то сразу станет ясно, что распределение количества детей определяется известным процессом рождения и гибели (см. [196]).

Фундаментальным следствием этого наблюдения является существование для величины <N> критического значения: этот факт был открыт в 1845 году Иренеем Бьянеме (см. [212]) и вполне заслуженно называется эффектом Бьянеме.

Значение <N>=1 является критическим в том смысле, что количество N(m) наличествующих в m - м поколении отпрысков ставит нас перед очень простой альтернативой. Если <N>?1, то семейство почти наверняка вымрет, и в настоящей интерпретации это означает, что каскад даст, в конце концов, пустое множество. Если же <N>>1, то генеалогическая линия каждого творога имеет ненулевую вероятность продолжиться на бесконечное число поколений. В этом случае случайное створаживание дает в пределе случайную линейную пыль.

Смысл размерности подобия. Так как отношение lnN(m)/ln(1/r) здесь изменяется случайным образом, понятие размерности подобия требует переосмысления. Из почти истинного соотношения

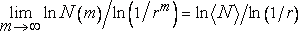
можно предположить, что обобщенная размерность подобия выглядит следующим образом:

D^*=ln<N>/ln(1/r)=E?lnp/ln(1/r).

При таком определении D^* условие существования непустого предельного множества <N>>1 принимает весьма логичный вид: D^*>0. Если D^*>0, то D=D^*. Если же мы формально применим эту формулу к случаю <N>?1, то получим D?0, однако фактически размерность D пустого множества всегда равна 0.